Definition, Solved Example Problems - Principal Value of Inverse Trigonometric Functions | 12th Mathematics : UNIT 4 : Inverse Trigonometric Functions
Chapter: 12th Mathematics : UNIT 4 : Inverse Trigonometric Functions
Principal Value of Inverse Trigonometric Functions
Principal Value of Inverse Trigonometric Functions
Let us recall that the principal value of a inverse
trigonometric function at a point x is the value of the inverse function
at the point x , which lies in the range of principal branch. For
instance, the principal value of cos−1 (√3/2) is π/6. Since π /6 ∈
[0, π].
When there are two values, one is positive and the other is
negative such that they are numerically equal, then the principal value of the
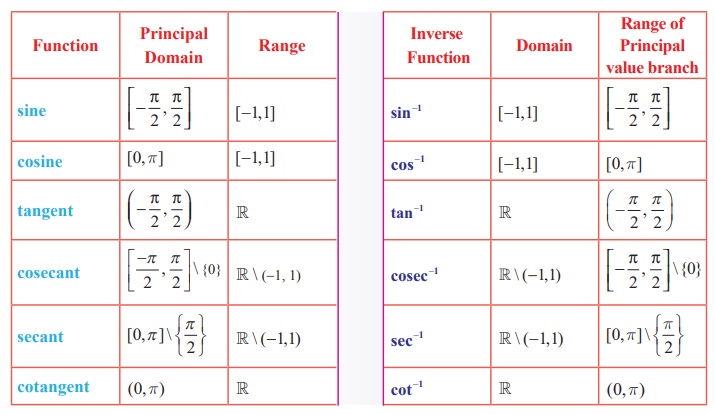
inverse trigonometric function is the positive one. Now, we list out the principal domain and range of trigonometric
functions and
the domain and range of inverse trigonometric
functions.
Example 4.12
Find the principal value of
(i) cosec-1 (-1) (ii) sec-1 (-2) .
Solution
(i) Let cosec-1 (-1) = y . Then, cosec y = -1
Since the range of principal value branch of y= cosec-1 x is [- π/2
, π/2] \ {0} and
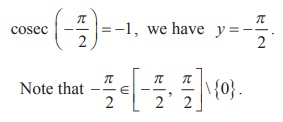
Thus, the principal value of cosec-1 (-1) is – π/2 .
(ii) Let y = sec-1 (-2) . Then, sec y = -2 .
By definition, the range of the principal value branch of y = sec-1 x is [0,π ]\ {π /2} .
Let us find y in [0,π ] – {π/2} such that
sec y = -2 .
But, sec y = −2 ⇒ cos y = − 1/2 .
Now, cos y =- 1/2 = -cos π/3 = cos (π – π/3 ) = cos 2π/3 .
Therefore, y = 2π/3 .
Since 2π/3 ∈ [0, π ] \ {π/2 } , the
principal value of sec-1 (-2) is 2π/3 .
Example 4.13
Find the value of sec-1(- 2√3 / 2)
Solution

Example 4.14
If cot-1 ( 1/7 ) = θ , find the value of cos θ .
Solution
By definition, cot−1 x ∈ (0, π) .
Therefore, cot-1 (1/7) = θ implies cot θ ∈ (0,π ) .
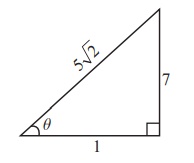
But cot-1 ( 1/7 ) = θ implies cot θ = 1/7 and hence tan θ = 7 and θ is
acute.
Using tan θ = 7/1 , we construct a right triangle as shown . Then,
we have, cosθ = 1/ 5√2 .
Example 4.15
Show that 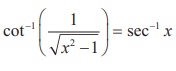 , x > 1 .
, x > 1 .
Solution
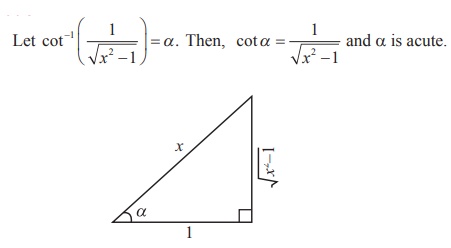
We construct a right triangle with the given data.
From the triangle, secα = x/1 = x . Thus, α = sec-1 x .
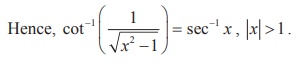
Related Topics