Cosecant Function and the Inverse Cosecant Function

The Cosecant Function and the Inverse Cosecant Function

Like sine function, the cosecant function is an odd function and has period 2π . The values of cosecant function y = cosec x repeat after an interval of length 2π .Observe that y = cosec x = 1/sinx  is not defined when sin x = 0 . So, the domain of cosecant function is R\ {nπ : n ∈ Z}. Since −1 ≤ sin x ≤ 1 , y = cosec x does not take any value in between −1 and 1. Thus, the range of cosecant function is (−∞,1] ∪[1, ∞) .

1. Graph of the cosecant function

In the interval (0, 2π ) ,  the  cosecant function  is continuous everywhere except at the point  x = π. It has neither maximum nor minimum. Roughly speaking, the value of y = cosec x falls from ∞ to 1 for x ∈ (0, π/2], it raises from 1 to ∞ for x∈ [π/2, π). Again, it raises from −∞ to -1 for x∈ (π, 3π/2]  and falls from -1 to −∞ for x ∈ [3π/2, 2 π).

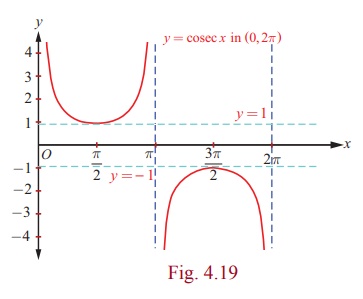
The graph of y = cosec x, x ∈(0, 2π ) \ {π } is shown  in  the  Fig.  4.19. This  portion  of  the  graph is repeated  for  the  intervals …, (−4π , − 2π ) \ {−3π }, (−2π , 0) \ {−π }, (2π , 4π ) \ {3π }, (4π , 6π ) \ {5π },…...

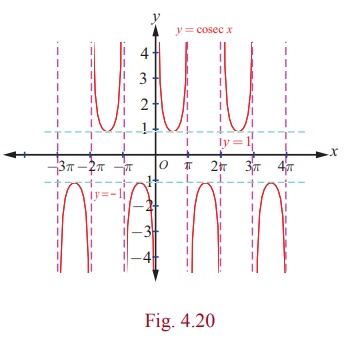
The entire graph of y = cosec x is  shown  in Fig. 4.20.

2. The inverse cosecant function

The cosecant function, cosec : [- π/2 , 0 ) U ( 0, π ] → (-∞, -1]  U [1, ∞) is bijective in the restricted domain [- π , 0 ) U ( 0, π ] . So, the inverse cosecant function is defined with the domain (-∞, -1] U [1, ∞) and the range [- π , 0 ) U ( 0, π ] .

Definition 4.6

The inverse cosecant  function cosec^-1 : (-∞, -1]  U  [1, ∞) →  [ - π /2 , 0)  U ( 0, π/2]  is defined by cosec^-1  (x) = y  if and only if cosec y = x  and y ∈ [ - π/2, 0)  U ( 0, π/2].

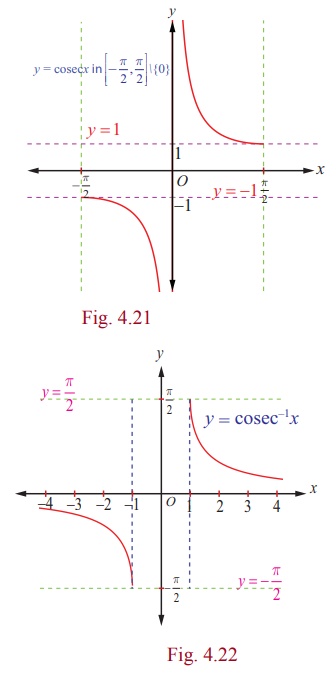
3. Graph of the inverse cosecant function

The inverse cosecant function, y = cosec^-1 x is a function whose domain is R \ (- 1, 1) and the range is [- π/2, π/2 ] \ {0}. That is, cosec^-1 : (-∞, -1] U [1, ∞) → [- π , 0 ) U ( 0, π ] .

Fig. 4.21 and Fig. 4.22 show the graphs of cosecant function in the principal domain and the inverse cosecant function in the corresponding domain respectively.