The Cosine Function and Inverse Cosine Function

The Cosine Function and Inverse Cosine  Function

The cosine function is a function with R as its domain and [−1, 1] as its range. We write y = cos x and  y = cos⁻¹  x  or  y = arccos(x)  to represent the cosine function and the inverse cosine function, respectively.  Since  cos ( x + 2π ) = cos x  is true for all real numbers  x  and  cos ( x + p) need not be equal to cos x for 0 < p < 2π , x ∈ R , the period of y = cos x is 2π.

1. Graph of cosine function

The graph of cosine function is the graph of y = cos x , where x is a real number. Since cosine function is of period  2π , the graph of cosine function is repeating the same pattern in each of the intervals  …., [−4π , − 2π ] , [ − 2π , 0] ,  [0, 2π ] , [2π , 4π ] , [4π , 6π ] , ….  . Therefore, it suffices to determine the portion of the graph of cosine function for x ∈ [0, 2π ] . We construct the following table to identify some known coordinate pairs (x, y) for points on the graph of y = cos x , x ∈ [0, 2π ].

The table shows that the graph of  y = cos x ,  0 ≤ x ≤ 2π , begins at (0,1). As x increases from 0 to π , the value of  y = cos x decreases from 1  to  −1 . As  x  increases from π  to  2 π , the value of  y increases from −1 to 1. Plot the points listed in the table and connect them with a smooth curve. The portion of the graph is shown in Fig. 4.10.

The graph of y = cos x , x ∈ R consists of repetitions of the above portion on either side of the interval [0, 2π ] and is shown in Fig. 4.11. From the graph of cosine function, observe that cos x is positive in the first quadrant (for 0 ≤ x ≤ π/2), negative in the second quadrant ( for π/2 < x ≤ π) and third quadrant ( for π < x < ≤ 3π/2) and again it is positive in the fourth quadrant ( for 3π / 2 < x < 2π).

Note

We see from the graph that cos(− x ) = cos x for all x , which asserts that y = cos x is an even function 

2. Properties of the cosine function

From the graph of y = cos x , we observe the following properties of cosine function:

1.        There is no break or discontinuities in the curve. The cosine function is continuous.

2.        The cosine function is even, since the graph is symmetric about y -axis.

3.        The maximum value of cosine function is 1 and occurs at x =… , − 2π , 0, 2π , … and the minimum value is − 1 and occurs at x =… , − π , π , 3π , 5π , …. . In other words, −1≤ cos x ≤1 for all x ∈  R .

Remark

(i) Shifting the graph of y = cos x to the right π/2 radians, gives the graph of y = cos ( x – π/2 ) , which is same as the graph of y = sin x . Observe that cos ( x – π/2 ) = cos ( π/2 - x ) = sin x .

(ii) y = A sin α x and y = B cos β x always satisfy the inequalities – |A| ≤ A sin α x ≤ |A| and - |B| ≤ B cos β x ≤ |B| . The amplitude and period of y = A sin α x are |A| and 2π/|α| , respectively and those of y = B cos β x are |B| and 2π/|β| , respectively.

The functions y = A sin α x and y = B cos β x are known as sinusoidal functions.

(iii) Graphing of y = A sin α x and y = B cos β x are obtained by extending the portion of the graphs on the intervals [0 , 2π/|α| ] and [0, 2π/|β| ] , respectively.

Applications

Phenomena in nature like tides and yearly temperature that cycle repetitively through time are often modelled using sinusoids. For instance, to model tides using a general form of sinusoidal function y = d + a cos (bt − c) , we give the following steps:

(i) The amplitude of a sinusoidal graph (function) is one-half of the absolute value of the difference of the maximum and minimum y -values of the graph.

Thus, Amplitude , a = 1/2 ( max − min)  ;  Centre line is  y = d , where d = 1/2 ( max + min)

(ii) Period, p = 2 × ( time from maximum to minimum) ; b = 2π/p

(iii) c = b × time at which maximum occurs.

Model-1

The depth of water at the end of a dock varies with tides. The following table shows the depth ( in metres ) of water at various time.

Let us construct a sinusoidal function of the form y = d + a cos (bt - c) to find the depth of water at time t. Here,  a = 1.4  ;  d = 2.8  ;   p = 12  ;  b = π/6   ;  c = π /3.

The required sinusoidal function is y = 2.8 +1.4 cos( π/6  t – π/3 )

Note

The transformations of sine and cosine functions are useful in numerous applications. A circular motion is always modelled using either the sine or cosine function.

Model-2

A point rotates around a circle with centre at origin and radius 4. We can obtain the y -coordinate of the point as a function of the angle of rotation.

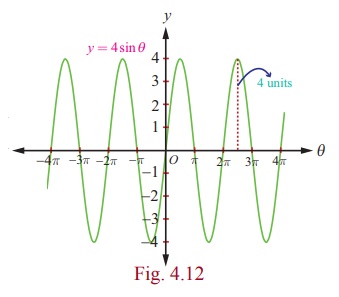
For a point on a circle with centre at the origin and radius a, the  y -coordinate of the point  is   y = a sinθ , where  θ  is the angle  of rotation.  In  this  case,  we  get  the  equation y(θ ) = 4 sinθ , where θ is in radian, the amplitude is 4 and the period is 2π  . The amplitude 4 causes a vertical stretch  of the y -values of the function sin θ by a factor of 4.

3 .The inverse cosine function and its properties

The cosine function is not one-to-one in the entire domain R . However, the cosine function is one-to-one on the restricted domain [0, π ] and still, on this restricted domain, the range is [−1, 1]. Now, let us define the inverse cosine function with [−1, 1]as its domain and with [0, π ] as its range.

Definition 4.4

For -1 ≤ x ≤ 1,  define cos^-1 x as the unique number  y  in [0, π] such that cos y = x . In other words, the inverse cosine function  cos^-1 : [-1, 1] → [0, π] is defined by  cos^-1 (x) = y  if and only if cos y = x and y ∈[0, π ].

Note

(i) The sine function is non-negative on the interval [0, π ], the range of cos⁻¹ x . This observation is very important for some of the trigonometric substitutions in Integral Calculus.

(ii) Whenever we talk about the inverse cosine function, we have cos x : [0, π ] → [−1, 1] and cos⁻¹ x : [−1, 1] → [0, π ] .

(iii) We can also restrict the domain of the cosine function to any one of the intervals …,[−π , 0],[π , 2π ],…., where it is one-to-one and its range is [−1, 1].

The restricted domain [0, π ] is called the principal domain of cosine function and the values of y = cos⁻¹ x , −1 ≤ x ≤ 1, are known as principal values of the function y = cos⁻¹ x .

From the definition of y = cos⁻¹ x , we observe the following:

(i) y = cos^-1x if and only if x = cos y for -1 ≤ x ≤ 1 and 0 ≤ y ≤ π .

(ii) cos (cos^-1  x) = x  if |x| ≤  1 and has no sense if |x| > 1 .

(iii) cos^-1 (cos x) = x if 0 ≤ x ≤ π , the range of cos^-1 x . Note that cos^-1 (cos 3π ) = π .

4. Graph of the inverse cosine function

The inverse cosine function  cos^-1 : [-1, 1] →[0, π ], receives a real number  x  in the interval [−1, 1]  as an input and gives  a real number   y  in the interval  [0, π ]as an output (an angle in radian measure).  Let  us  find  some points (x, y) using the equation y = cos^-1 x and plot them in the xy -plane. Note that the values of y decrease from π to 0 as x increases from -1 to 1. The inverse cosine function is decreasing and continuous in the domain. By connecting the points by a smooth curve, we get the graph of y = cos^-1 x as shown in Fig. 4.14

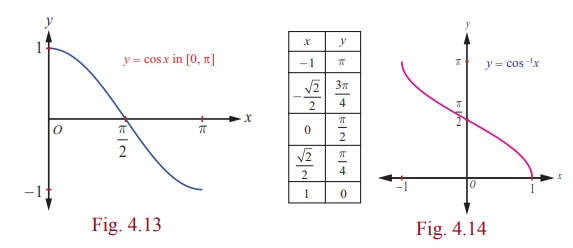
Note

(i) The graph of the function y = cos^-1 x is also obtained from the graph y = cos x by interchanging  x and y axes.

(ii) For the function y = cos^-1 x , the x -intercept is 1 and the y -intercept is π/2 .

(iii) The graph is not symmetric with respect to either origin or y -axis. So, y = cos^-1 x is neither even nor odd function.

Example 4.5

Find the principal value of cos^-1 ( √3 / 2 ) .

Solution

Let cos^-1 (√3 / 2 ) = y . Then, cos y = √3 / 2.

The range of the principal values of y = cos^-1 x is [0, π ].

So, let us find y in [0, π ] such that cos y = √3 / 2

But, cos π/6 =  √3/2   and  π/6 ∈ [0,π ]. Therefore,  y = π /6

Thus, the principal value of cos^-1 (√3/2 ) is π/6 .

Example 4.6

Find 

Solution

It is known that cos^-1 x : [-1, 1] → [0, π ] is given by 

cos^-1 x = y if and only if x = cos y for -1 ≤ x ≤ 1 and 0 ≤ y ≤ π .

Thus, we have 

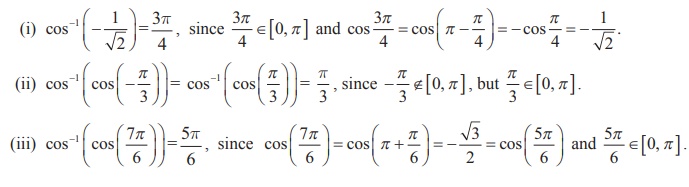
Example 4.7

Find the domain of cos^-1 ( [2 + sin x] /3 ) .

Solution

By definition, the domain of y = cos^-1 x  is -1 ≤ x ≤ 1 or |x| ≤1 . This leads to 

-1 ≤  [2 + sin x]/3 ≤ 1 which is same as - 3 ≤ 2 + sin x ≤ 3 .

So, - 5 ≤ sin x ≤ 1  reduces to -1 ≤ sin x ≤ 1, which gives 

- sin^-1 (1) ≤ x ≤ sin^-1 (1) or  π/2 ≤ x ≤ π/2 .

Thus, the domain of cos^-1 ( [2 + sin x] /3 )  is [- π/2 , π/2 ] .