Problem Questions with Answer, Solution - Exercise 4.5: Inverse Trigonometric Functions | 12th Mathematics : UNIT 4 : Inverse Trigonometric Functions
Chapter: 12th Mathematics : UNIT 4 : Inverse Trigonometric Functions
Exercise 4.5: Inverse Trigonometric Functions
Maths Book back answers and solution for Exercise questions - Mathematics : Inverse Trigonometric Functions: Exercise Questions with Answer, Solution
EXERCISE 4.5
1. Find the value, if it exists. If not, give the reason for non-existence.
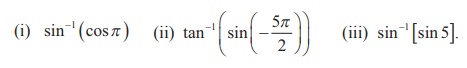

2. Find the value of the expression in terms of x , with the help of a reference triangle.



3. Find the value of
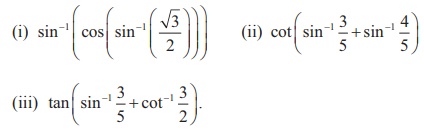



4.Prove that
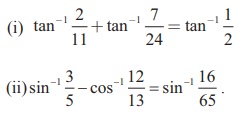


5.Prove that tan−1 x + tan−1 y + tan−1 z = tan−1 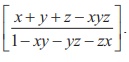

6. If tan−1 x + tan−1 y + tan−1 z = π , show that x + y + z = xyz .

7. Prove that 

8.Simplify 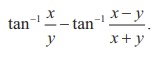

9. Solve:
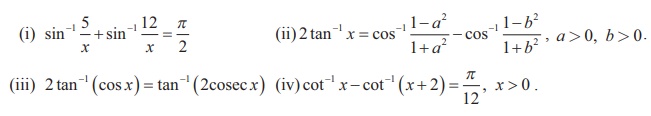



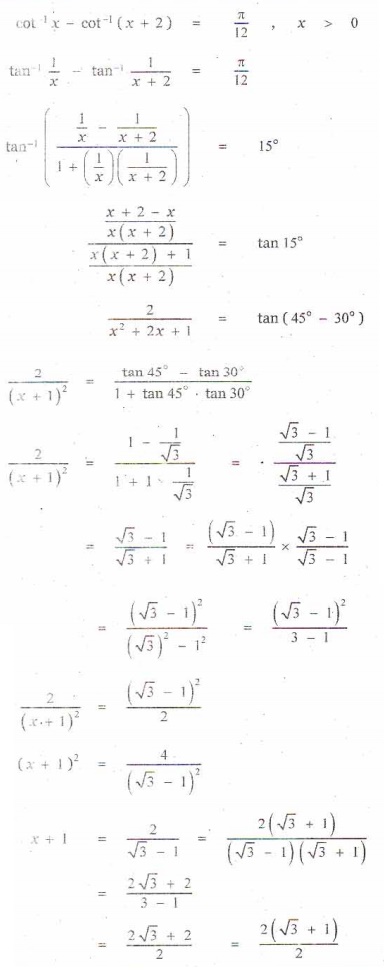

10. Find the number of solution of the equation tan-1 ( x -1) + tan-1 x + tan-1 ( x +1) = tan-1 (3x).
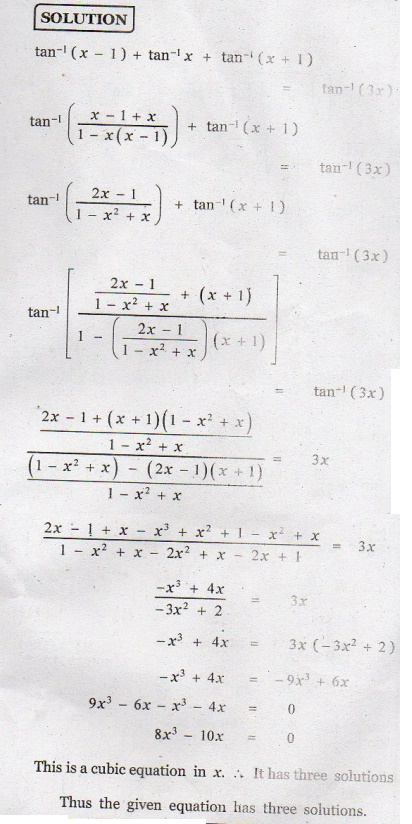
Answers:
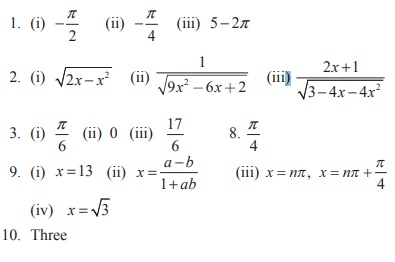
Tags : Problem Questions with Answer, Solution , 12th Mathematics : UNIT 4 : Inverse Trigonometric Functions
Study Material, Lecturing Notes, Assignment, Reference, Wiki description explanation, brief detail
12th Mathematics : UNIT 4 : Inverse Trigonometric Functions : Exercise 4.5: Inverse Trigonometric Functions | Problem Questions with Answer, Solution
Related Topics
12th Mathematics : UNIT 4 : Inverse Trigonometric Functions