The Secant Function and Inverse Secant Function

The Secant Function and Inverse Secant Function

The secant function is defined as the reciprocal of cosine function. So, y = sec x=1/cosx is defined for all values of x except when cos x = 0 .Thus, the domain of the function y = sec x is  .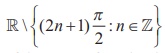

As −1 ≤ cos x ≤ 1, y = sec x does not take values in (−1, 1) . Thus, the range of the secant function is (−∞,1] ∪[1, ∞) . The secant function has neither maximum nor minimum. The function y = sec x is a periodic function with period 2π and it is also an even function.

1. The graph of the secant function

The graph of secant function in 0 ≤ x ≤ 2 π,  x≠ π/2, 3π/2 is shown in Fig. 4.23.

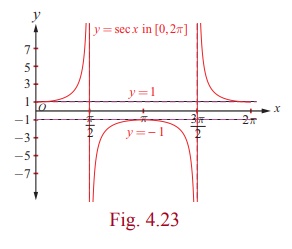
In the first and fourth quadrants or   in   the interval – π/2 < x < π/2, y = sec x   takes   only   positive  values, whereas it takes only negative values in the second and third quadrants or in the interval π/2 < x < 3π / 2.

For 0 ≤ x ≤ 2 π , x ≠ π/2, 3π/2, the secant function is continuous. The value of secant function raises from 1 to ∞ for x ∈ [0, π/2);  it raises from −∞ to −1 for x ∈ (π/2, π]. It falls from −1 to −∞ for x∈ [π , 3 π /2) and falls from ∞ to 1 for x∈ (3 π/2, 2 π].

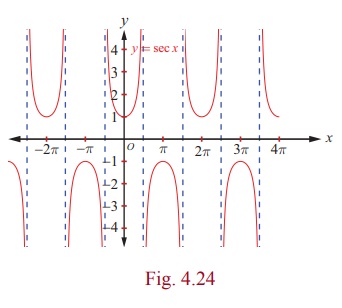
As y = sec x is periodic with period 2π , the same segment of the graph for 0  ≤ x ≤ 2π , x ≠ π/2, 3 π/2, is repeated in 

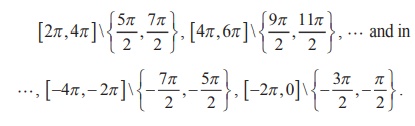
Now, the entire graph of y = sec x is shown in Fig. 4.24.

2. Inverse secant function

The secant function, sec x : 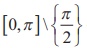→ R \ (−1,1)  is bijective in the restricted domain .

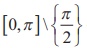So, the inverse secant function is defined with R \ (−1,1) as its domain and with 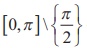 as its range.

Definition 4.7

The secant function, sec-1 : R\(-1, 1) → [0,π ] \ {π/2} is defined by sec-1 (x) = y whenever sec y = x and y ∈[0,π ] \ {π/2 } .

3. Graph of the inverse secant function

The inverse secant function, y = sec−1 x is a function whose domain is R \ (−1,1) and the range is 

[ - π/2, π/2]\{0}. That is, cosec-1 : (-∞, -1] U [1, ∞) → [ - π/2, 0) U (0, π/2].

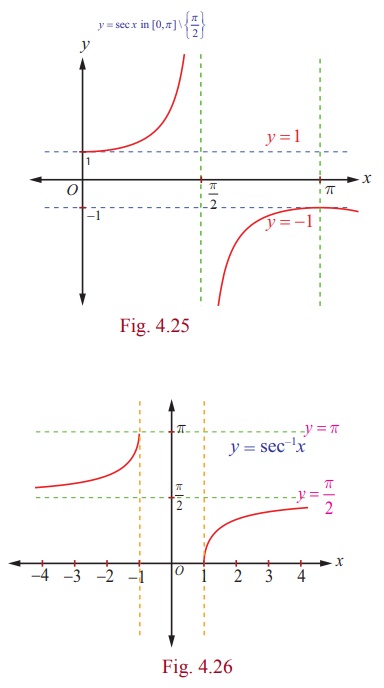
Fig. 4.25 and Fig. 4.26 are the graphs of the secant function in the principal domain and the inverse secant function in the corresponding domain, respectively.

Remark

A nice way to draw the graph of y = sec x or cosec x :

(i) Draw the graph of y = cos x or sin 

(ii) Draw the vertical asymptotes at the x -intercepts and take reciprocals of y values