Chapter: Civil : Principles of Solid Mechanics : Slip Line Analysis
Slopes and Footings
Other Special Cases: Slopes and Footings
As in the elastic range,
the general solution for a general wedge at the limit state can be applied to
special cases of particular interest. Consider first a free slope (Figure
12.13a) where there is no wall to help restrain the sliding. Since T =
0,
cos (2Žł + 2╬▓)
=
0
and therefore the slip surface is unique
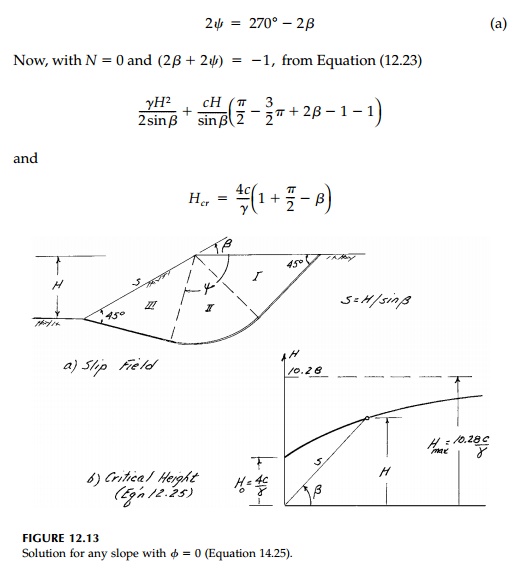
Since there is no
closedform elasticity solution for a slope loaded by its own weight, this
result is particularly important in that at least the stress field at collapse
is known to the designer.
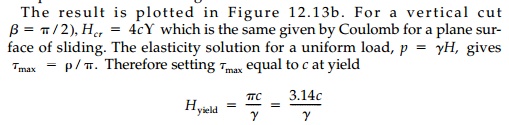
and, for a vertical
slope, there is little load capacity beyond first yield.
At
the other extreme, as ╬▓ approaches zero (a
very gentle slope), Žł approaches
135┬ o and Hcr =10.28/╬│.
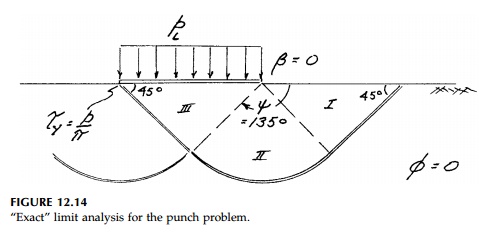
We have also, in fact,
finally derived the exact limitload solution for the footing problem for which
upperbound estimates were made using circular and sliding block mechanisms. The
solution for the passive case for a wall at ╬▓= 0 gives it to us directly. If we assume a smooth footing (the wall) then from
Equation (12.25),
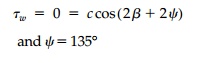
135┬ o giving the failure
mechanism as shown in Figure 12.14. The normal stress on the wall is the
uniform distributed limit load pL so
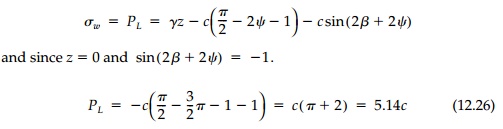
This is considered the correct solution. The ŌĆ£bestŌĆØ circular and slidingblock mechanisms from previews pages give pL == 5.7c illustrating the upperbound theorem. The symmetry of the correct slip surface shows why the unit weight drops out of the expression for pL when ŽĢ=0.
Example 12.4
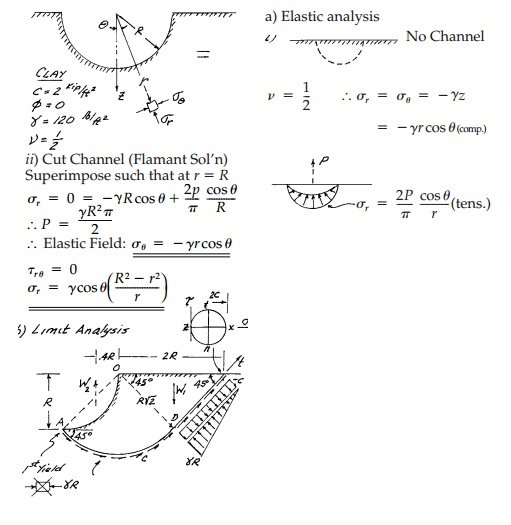
A long semicircular channel with radius R
is to be cut from an elastic, perfectlyplastic, incompressible halfspace.
a. Solve
for the elastic stress field before the channel is filled with water and
thereby determine the factor of safety against yield. Assume plane strain.
b. Estimate
the limit load (i.e., the critical limiting radius RL for collapse)
and compare to the yield radius RY.

Related Topics