Comparison to the Coulomb Solution (Ï•=0)

Comparison to the Coulomb Solution (Ï•=0)

Let us now investigate limiting cases and then compare results to the Coulomb solution for a vertical wall with no interface friction.

From Equations (12.23) and (12.24) for

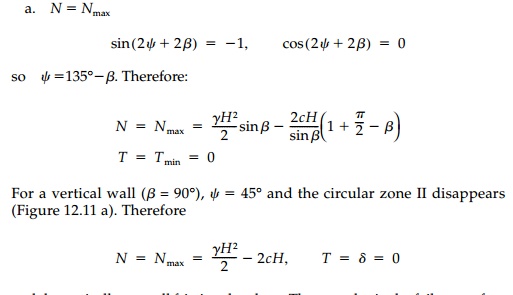
and theoretically no wall friction develops. Thus we obtain the failure surface and stress distribution identical to Coulomb's solution, Ïƒ_w = Î³z - 2c and Ï„_w = 0, plotted in Figure 12.5 as line ge.

At the other extreme for:

b.    N = N_min ;   T = T _max

for a very rough wall along which the shear strength is fully mobilized. Thus T, N, and Î´ are functions of Ïˆ, which defines the failure surface.

In practice, however, the average angle of wall friction, Î´, is usually selected on the basis of the possibilities of wall movement and the relative roughness of the wall (e.g., steel is relatively smooth compared to concrete). For a known  Î´, T, N, P, the angle Ïˆ  and the point of application of the resultant thrust are uniquely defined. The complete solution for a vertical wall is shown in Figure 12.12 where it can be seen that wall friction always helps both by reducing P_A and lowering the point of its application. The total thrust for Î´=0 given by Coulomb is a maximum. Friction is often neglected in design in soil mechanics to help compensate for the unsafe assumption of tension capacity in the upper portion of the active wedge.