Retaining Wall Solution for (EPS Material)

Retaining Wall Solution for  (EPS Material)

First let us consider a wedge as shown in Figure 12.9 where for simplicity we will assume the top surface, BC, is free of boundary tractions and there is a rigid retaining wall supporting the EPS material with unit weight γ on the sloping face AB. If the wall moves outward in the direction of the v arrows, the active state of limiting equilibrium develops. A general failure surface, which by our analysis is a combination of straight and circular segments, is assumed. This is a combination of an upper wedge (slip field I) with plane surfaces of sliding, a circular transition section, II, and a third wedge, III, adjoining the wall.

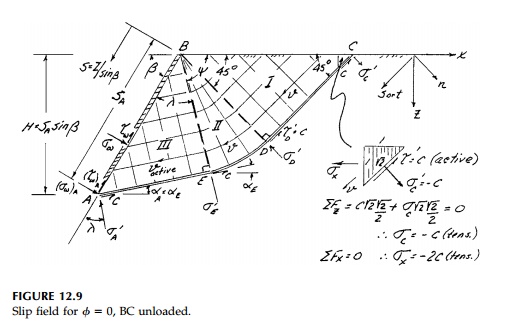
Since we do not know the extent of slip fields II and III or the stresses on the wall, we cannot solve directly but must work our way along the slip surface* from the known boundary, BC, to the unknown boundary, AB, using the solution [Equation (12.15)] to Kötter’s equation for ϕ= 0. Starting at point C we know the complete state of stress. Since τ_xz=σ_z = 0, x and z are principal directions and therefore α = 45º. From Mohr’s Circle and the direction of τ' for the active case, σ' =- c, τ' = c and from Equation (12.15)

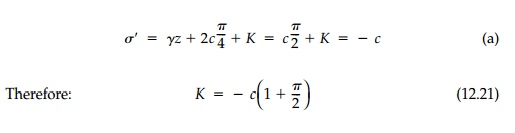
As we move to point D, x and z remain principal so σ'_D = γz_o - c, τ'= c. However, from D to E on the circular portion of the failure surface, α changes as well as the depth so

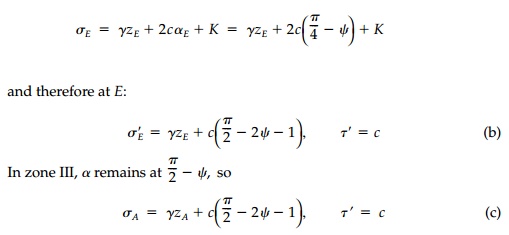
Therefore at A in the orientation of the wall, the stresses on the wall from Mohr's Circle are:

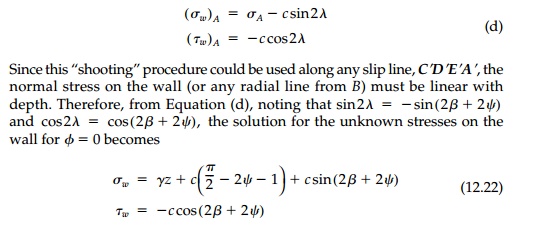
It is important to note that the actual values of the wall stresses depend on the choice of ψ, which specifies the extent of the circular zone II. The distribution of stress on the wall however, is determined by the solution to be a constant shear and a normal stress linear with depth. Any other distribution cannot be specified for a unique solution to this Cauchy problem and maintain the unloaded boundary conditions on the surface BC.*

The direction of the resultant stress on the wall varies since the normal stress increases with depth while the shear stress is constant. Therefore, to talk about a constant “angle of wall friction” δ is a misnomer. However, we can compute the components of the force resultants on the wall by integrating the stresses, i.e.,

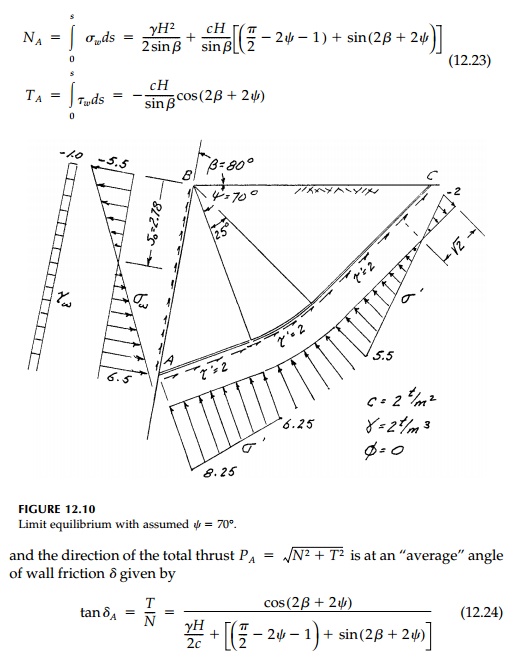
A specific example to illustrate this complete stress solution at limit equilibrium for the case ψ=70� o is shown in Figure 12.10. For the passive case where the wall is forced into the material, the failure surface is the same but the direction of impending motion is revised. Thus the shear stress on the failure surface acts in the opposite direction to resist the

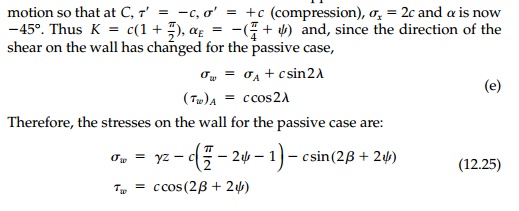
This is the same result as for the active case except that the constants by which the geostatic normal stress γz is modified have changed sign, as has the shear. The shear resultants N, T are modified accordingly as is the average angle of wall friction.