Graphic Analysis and Minimization

Graphic Analysis and Minimization

In his paper, Coulomb only derives the active pressure Equation (12.3b). However, although not stated explicitly, this implies both the basic MohrCoulomb strength criterion, Equation (3.16) and the passive pressure Equation (12.3a). The actual method Coulomb used to obtain the minimum active and maximum passive forces was graphical. Developed in greater detail by Culmann*, Example 12.2 presents the method for the active case. For any straight slipline trial,** a force diagram can be drawn as in Figures 12.4c and d. By plotting a number of trials superimposed, the maximum can be seen directly. This is similar in every respect to the onedimensional problem of the collapse of an indeterminate beam as in Figure 11.5 where a graphical minimization is used to determine the limit load and position of the plastic hinges (critical collapse mechanism) simultaneously. For retaining walls, however, the computation of the thrust for each trial is also done graphically.

For homogeneous cases with c = 0, straight boundaries, and no external loading, the forces can be expressed in terms of the geometric variables Î², i, and friction angles Î´, Ï• to obtain a closed form expression for P. This can be formally minimized or maximized to obtain formulas for the active and passive thrusts and the critical straightline slip surfaces associated with them. These will be given in the concluding section of this session.

However, the graphical method for any particular case is very quick and much more general. With the basic assumption of a straight slip surface, any shaped wall, wall roughness, backfill geometry, layered backfill with discontinuous c, Ï•, Î³, condition of the water table, or practically any other complexity can be included with very little additional work. Moreover, it is a design as much as an analysis approach. Thus Coulomb’s method of analysis, relying on successive applications of graphic statics, is as much of an accomplishment, in its way, as are his equations.

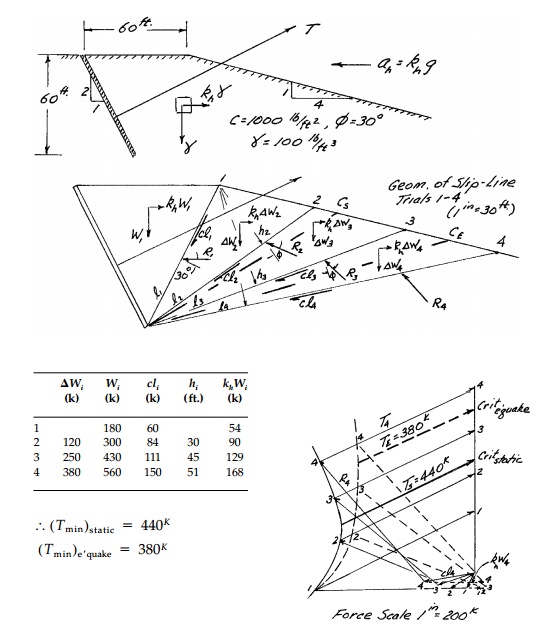
Example 12.3

a.  An anchor for a bridge tower is designed as shown below. Assume no wall friction and neglecting any active pressures behind the wall, determine the ultimate (limiting) static passive resistance T_L of the anchor.

b.Modify your analysis to include inertial forces due to an earthquake with a peak horizontal acceleration a_h = 0.3g. Show the difference between the seismic and static value for T_L and the critical seismic and static slip surfaces.