Slip Line Analysis: The General Case

The General Case

Unfortunately Kötter’s equation cannot be integrated directly for a closedform solution in the general case of a Coulomb material with weight or for nonconstant boundary loads. The most common numerical procedure for integrating Kötter ’s equation was developed by V.V. Sokolovski* where the integration proceeds from one boundary to the other in the direction of the characteristic slip lines using a finitedifference approximation. This shooting technique called “the method of characteristics” is necessary since, as already discussed, the governing equations are hyperbolic and, if the load is specified completely on the entire boundary, a solution will not normally exist.

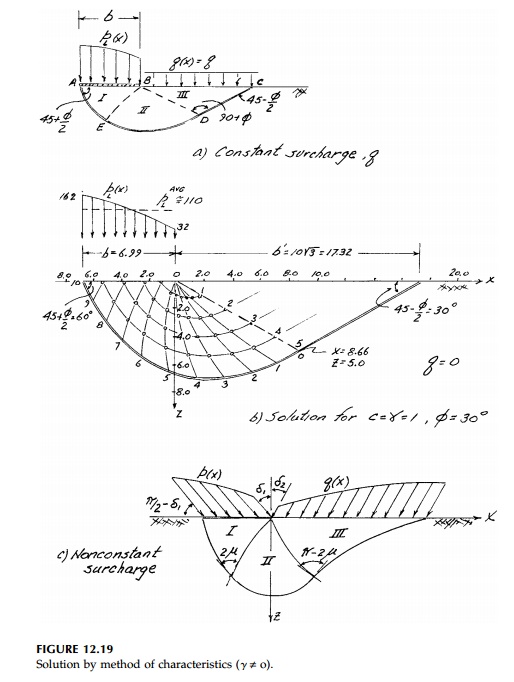
The result then may be an “exact” solution for the slip field but only approximate the load prescribed. Take for example the footing problem shown again in Figure 12.19. We would like to solve for the uniform load intensity p_L that will cause collapse by forcing the material to shear under the punch and bulge upward lifting the uniform surcharge q upward with the passive wedge of region I. The solution starts from the boundary BC on which σ_z = q = constant, τ_{xz =} 0, and b' is selected to some convenient scale. However, in this case region I is the passive Coulomb solution with σ₃ = q so the stresses on BD are known and we can actually start from there. Recurrence formulas for piecewise integration of Kötter’s equation along the characteristics in the fanshaped Region II and the Active Region III are derived by Sokolovski. The accuracy depends on how dense we make the finiteelement grid of characteristics (or slip lines).

The resulting slipline field and limit loading p(x) are shown in Figure 12.19b for a smooth, surface footing (q = 0) with c = γ = 1 and ϕ = 30º. Neither the width of the footing, b, nor the distribution of the limit load p_L can be specified in advance and we see that p_L is far from uniform. Thus we have a

method that we can make as accurate as we want to solve for the wrong load! One can use an equivalent limit load intensity

to approximate a uniform failure loading but that will still underestimate the capacity since the moment around 0 is less. Reversing the direction of the shooting technique does no good in that if p is specified constant, then q becomes a function of x.

If q is not constant, then as shown in Figure 12.19c, the slip surface s with γ != 0 is neither straight, a log spiral, or circular in any zone. A variety of solutions using the method of characteristics are presented in the literature for the bearing capacity problem, slopes, and retaining walls for a variety of surcharge distributions. Since these seldom correspond to realisticboundary conditions they are primarily of academic interest.

Another approach to the general problem is to incorporate the effect of weight using the same critical slip surface derived by Prandtl for γ=0. This cannot be correct, but a reasonable argument can be made that it is conservative. This is the approach used by Terzaghi* in presenting his general bearing capacity formula:

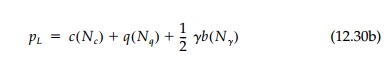
where Nγ like the other two “Bearing Capacity Factors” N_c and N_q, are functions of ϕ. The values for Nγ given in Table 12.1 for the Prandtl Mechanism are obtained from the approximation:

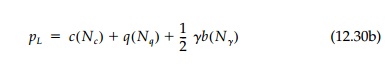
The power of the upperbound approach to limit analysis, however, is supposed to be the simplicity of the method. To return to this theme, let us conclude by introducing a simple failure mechanism based, for the bearing capacity problem, on Coulomb wedges, which is more versatile, easy for computation, and is intuitively satisfying.