An Approximate “Coulomb Mechanism”

An Approximate “Coulomb Mechanism”

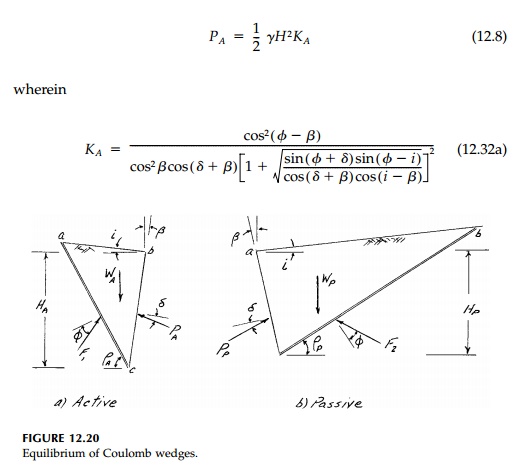
For the Coulomb wedge in the active case, the free body diagram for no cohesion is as shown in Figure 12.20a. Let i be the angle at which the surface of the backfill rises above the horizontal, β be the angle between the wall and the plane, which is vertical to the horizontal surface of the ground in front of the wall, and ρ_A be the angle between the failure surface and the horizontal.

From the force equilibrium of the failure wedge, the maximum value of P_A, the total force acting on the wall, is:

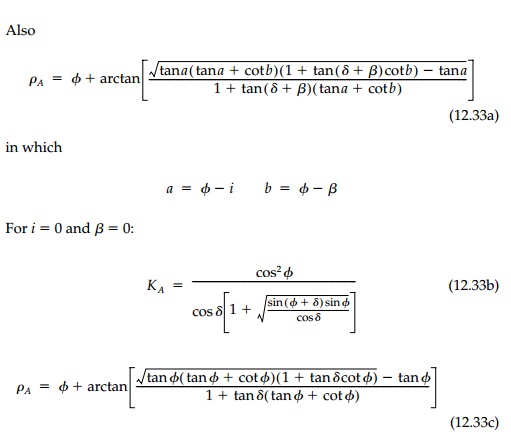
Similarly, the corresponding expression for the passive thrust (the free body diagram is shown in Figure 12.20b) is:

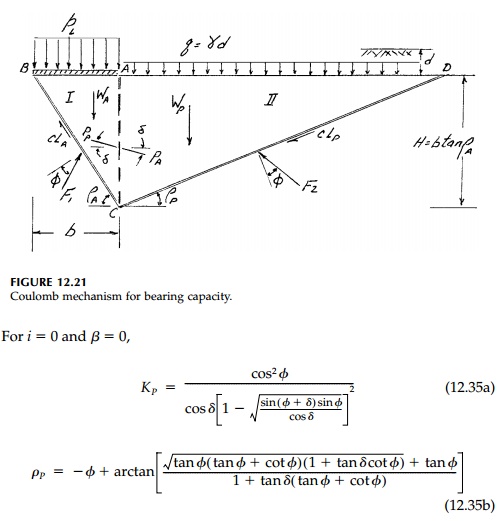
A very useful simplification of the Prandtl or Sokolovski failure surfaces is, as shown in Figure 12.21, to eliminate the fanshaped transition zone and thereby average its effect concentrating the shear transfer at AC. Line AC can then be thought of as a retaining wall with the active lateral thrust P_A from region I pushing against the passive resistance P_P from region III. From equilibrium of the two Coulomb wedges involved, bearingcapacity factors for each component of strength can be derived. Considering first the surcharge (c =  γ = 0)

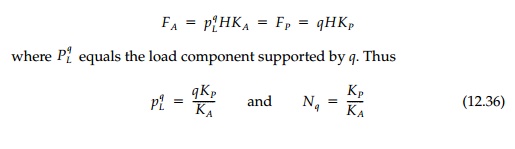
Similarly, considering only the contribution of the weight of the soil below the footing (q = c = 0), at collapse

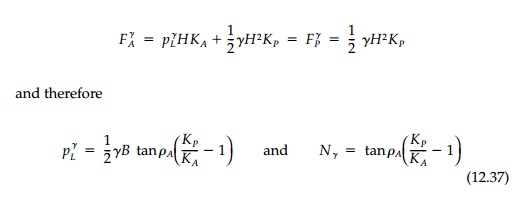
Finally, it might be noted that for only cohesion ( ϕ =0), equilibrium considerations of the Coulomb mechanism gives a value of N_c = 6.0, which is not unreasonable compared to the exact value of 5.14.

The corresponding staticbearing capacity factors N_q and Nγ for a granular soil for various values of ϕ and δ can now be calculated for the Coulomb mechanism from Equations (12.36) and (12.37) with the expressions for K_A, K_P, and ρ_A. The results are shown in Table 12.2 compared to the corresponding values for the Prandtltype mechanism and solution by the method of characteristics. For the correct kinematic Coulomb mechanism, the wedges must slip relative to each other and  δ=ϕ. This, by the upperbound theorem of limit analysis, must overestimate the bearing capacity, which it does. However, since the fictitious wall replaces the fanshaped transition zone, it should average the shear transfer, and setting  δ=ϕ/2 seems more reasonable as an approximation. As shown in Table 12.1, such an assumption for δ  does in fact give a very good correlation (± ~ 10%) between the mechanisms for all values of ϕ. The values for Nγ by the method of characteristics in Table 12.2 are those given by Sokolovski. His values seem to have been computed by simply taking the average

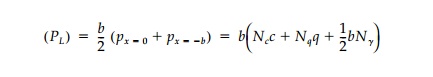
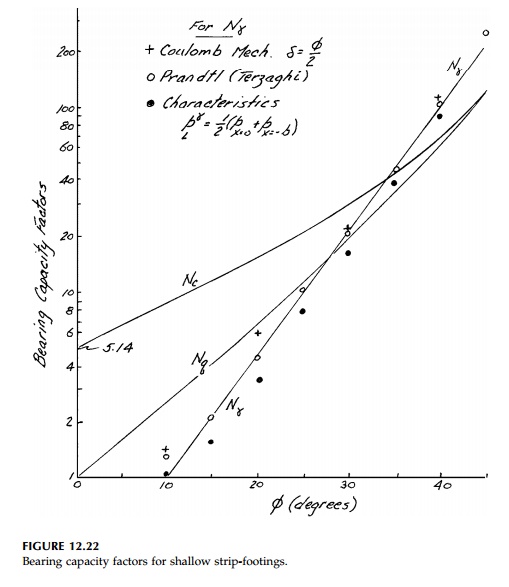
rather than computing the limit load P_L using the integral of the limit pressure distribution. Therefore, they are unnecessarily low since both the curvatures of the actual critical load intensity computed and its eccentricity are neglected. If we assume the distribution is parabolic, the value is ~15% higher, which is a better representation but still conservative. This modification is reflected in Figure 12.22 which gives the standard accepted value for bearing capacity factors for design of shallow strip footings.