Chapter: Civil : Principles of Solid Mechanics : Slip Line Analysis
Lateral ÔÇťPressuresÔÇŁ and the Retaining Wall Problem
Lateral ÔÇťPressuresÔÇŁ and the Retaining
Wall Problem
To further set the stage, let us look at the same
retaining wall problem that Coulomb considered as a young civil engineer in
charge of various construction projects on the island of Martinique in the
1760s. In order to address this problem, Coulomb first had to develop from
scratch the concepts of slip surfaces and limit analysis along with his law of
dry frictional resistance and cohesion.** Unfortunately, the information in his
1776 paper, while not obscure, is so condensed that it must be studied with
great attention and expanded to be appreciated. Coulomb was elected to the
academy in 1781 and never returned to soil mechanics and the retaining wall
problem, so his solution comes down to us as a few algebraic equations and two
small figures* with a minimum of explanation. It took nearly 200 years and
thousands of pages of text to recognize that his work includes all the concepts
and methodology needed for analysis and design of gravity retaining walls.
If we consider a vertical line (the wall) embedded in a MC halfspace (Figure 12.4a), the weight of the soil, Bz = ╬│, introduces the elastic stress field:
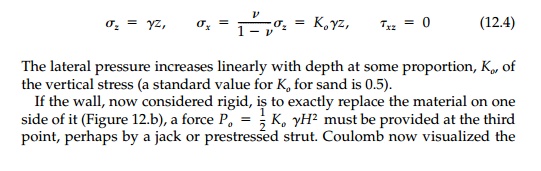
insights into such a
short space that, according to Poncelet, ÔÇťduring the next 40 years the attention
of engineers seemed not to focus on any of them.ÔÇŁ Perhaps because the
presentation of this paper in 1773 was his introduction to the French Academy
of Sciences, Coulomb felt intimidated as ÔÇťonly a practicing engineerÔÇŁ and kept
throwing in fundamental insight after insight with less and less explanation to
the point where the power of the whole obscures the beauty of the individual
parts. Certainly his introduction in which he states:
If I dare to present it (this paper) to this Academy
it is only because the feeblest endeavors are kindly welcomed by it when they
have useful objective . . .
would suggest he suffered
at this time from the same ÔÇťengineering inferiority syndromeÔÇŁ that Hooke
developed a century earlier trying to deal with NewtonÔÇÖs intolerable
egocentricity and wholesale theft of HookeÔÇÖs ideas in the name of science. In
fact, Coulomb amplifies this paranoia (probably justified) with further selfdenigration
noting that
ÔÇŽ while great men will be carried to the top of the
edifice (science) where they can mark out and construct the upper stories,
ordinary artisans (engineers) who are scattered through the lower stories ÔÇŽ.
should seek only to perfect that which cleverer hands have created.
Unfortunately, such nonsense is as prevalent a view
today as it was in HookeÔÇÖs and CoulombÔÇÖs time. * CoulombÔÇÖs figure (1776).
jacking force being gradually reduced and the wall
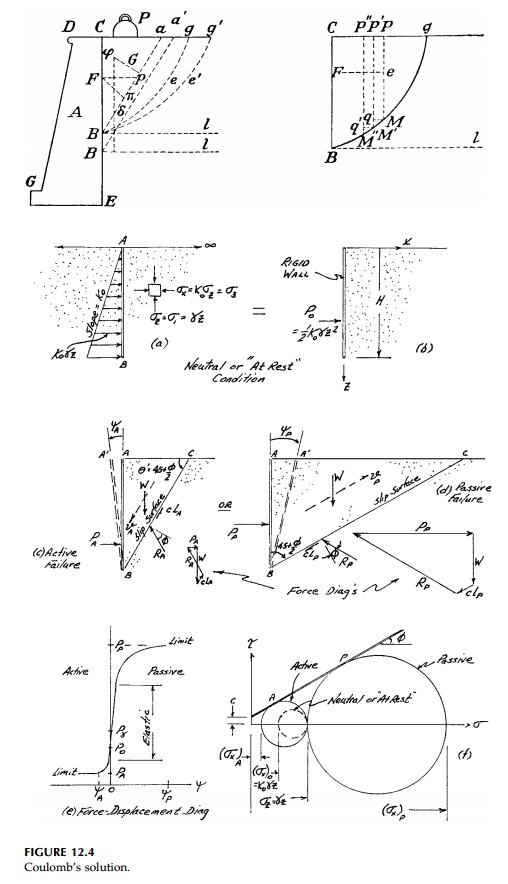
rotating about its base or translating slightly away from the soil so that the
shear strength could be mobilized to help support the soil (Figure 12.4c).
However, at some point when the shear strength is fully developed on some
slip surface, the material would slide downward and outward if the jacking
force were reduced further. The jacking force or the force necessary to just
prevent failure (sliding of the wedge), is the active force, PA.
If it is assumed that there is no wall friction then the stress field
[Equation (12.4)] is linear, the slip surface is straight,

If instead the wall is jacked into the soil, Figure 12.4d, the passive case develops where the friction mobilized in the soil again resists the motion but, in this case, adds to the jacking force necessary to cause failure. Again, if there is no wall friction, the slip surface will be straight and Equation (12.3a) applies with ¤â3 =╬│z = ¤âz (line ml in Figure 12.5 for c > 0, ¤Ľ > 0 ). Thus the passive
force PP just necessary to cause
the failure wedge to slide upward is
The amount of plastic
strain necessary to fully mobilize the shear strength and fully develop the
slip surface corresponding to either PA or PP
is uncertain. Yield may occur first at some point on the eventual slip surface
and then spread with continuing small movements of the wall until the complete
mechanism develops. In soils (to some extent rock and concrete) the issue is
further complicated in that not only does the shear strength depend on the
confining pressure, but also on the soilÔÇÖs density, the water content, and even
its history. Moreover, dense soils (and concrete) have a peak strength and then
a lower residual value at large strains (a strainsoftening material). Thus, the
complete active and passive curves for lateral load vs. deflection shown in
Figure (12.4e) are only approximate as far as values for the wall rotation ¤ł are concerned.
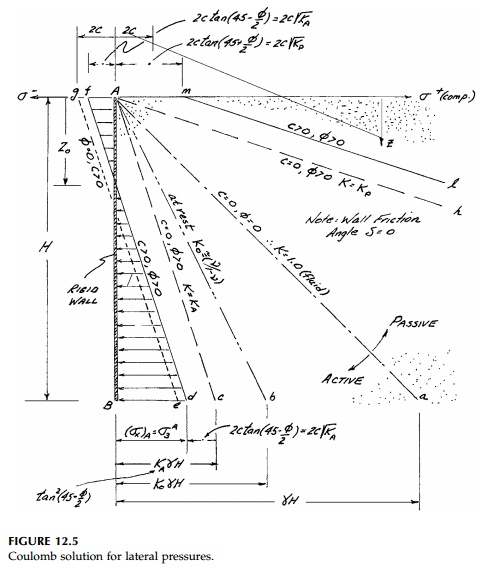
Eighty years later, Rankine,* considering the
retaining wall problem without regard to CoulombÔÇÖs solution, again assumed a
frictionless wall interface but also neglected cohesion. In rederiving
CoulombÔÇÖs equations he introduced coefficients of lateral pressure:
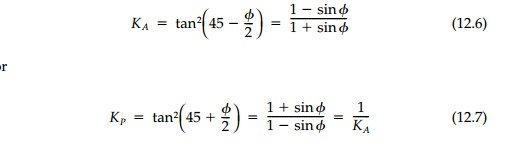
noting that, for such a special case of a purely
frictional material like sand, lateral pressures are like fluid pressure (a
heavy fluid) increasing linearly with depth as shown in Figure 12.5 lines Ac
and Ah. Thus ¤âh = ¤âx
=
Krz and the total active
or passive force on the wall will be:
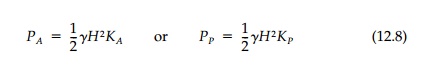
Related Topics