Mohr-Coulomb Criterion (Revisited)

Mohr-Coulomb Criterion (Revisited)

All materials have some component of frictional strength and therefore are stronger in compression than tension. For EPS materials (e.g., steel), this dif-ference is insignificant, but for cast iron, rock, concrete, or soil, frictional strength predominates and cannot be neglected. The Mohr-Coulomb crite-rion introduced in previews pages has the fundamental form:

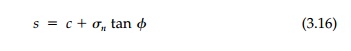
which plots as a straight line in stress space. Thus the shear strength, s, is a linear function of the normal stress σ_n on the potential slip plane where tan ϕ is the coefficient of friction.

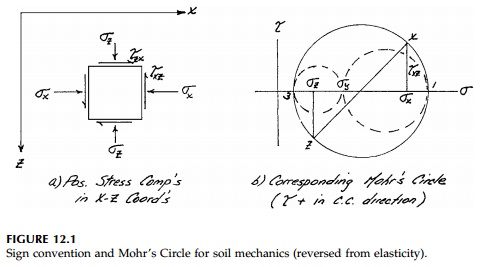
Since very “brittle” materials such as concrete have little tensile strength and granular materials like sand have none, we will, in this session pages, reverse the arbitrary sign conventions of elasticity. Thus, compression will be positive and shear stresses will be positive if the signs of the subscripts are mixed. The con-vention for plotting Mohr’s Circle is shown in Figure 12.1. Also, throughout, it will be assumed that we have a plane-strain situation where the out-of-plane normal stress, σ_y , is intermediate. That is:

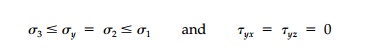
Therefore the slip planes on which τ' s are in the x�'z plane and only the largest Mohr’s Circle need be plotted in future figures.

One fundamental difference introduced by the M-C criterion is the possibility of two potential failure states and two sets of slip surfaces, “active” and “passive” at a point, even when one principal stress component is the same. This is easily seen in the triaxial “test” situation shown in Figure 12.2. Assuming this M-C material is initially at constant hydrostatic pressure σ_xⁱ + σ_zⁱ = p, the specimen can be brought to failure (Mohr ’s Circle touching the strength envelope) by either increasing σ_x (Figure 12.2a) or decreasing σ _x (Figure 12.2b) resulting in different sized and oriented Mohr Circles as shown in Figure 12.2c.

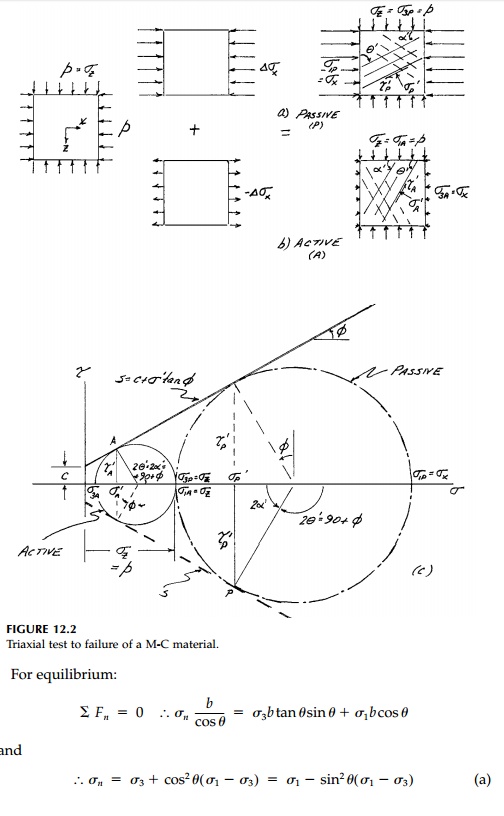
It is useful to go through a formal plastic analysis for either the active or passive case (although the result is obtained by simply drawing Mohr’s Circle touching the strength envelope as in Figure 12.2c). Consider, for example, the passive case illustrated again in Figure 12.3 where the stress field is constant (b any size). Note that the active case would give the same stressed element rotated 90� o where σ_x would now be the minimum principal stress and σ _z the major. Thus, in terms of the orientation of the principal stress components to the slip surfaces, there is no difference between the active and passive case.

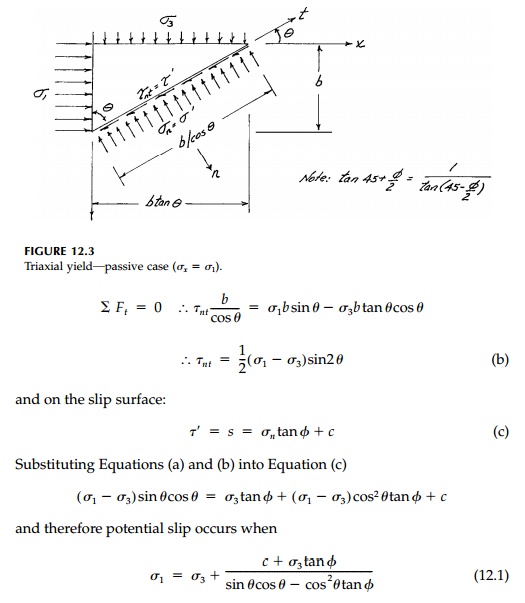
which apply in the principal stress orientation for either the active or passive case. Thus only when σ_x or σ_z is specified does the question arise of which “type of failure” occurs.

Finally, it is important to reemphasize that the block in Figure 12.3 can be thought of as a differential element (b = db) and therefore the analysis and equations are general for a point. However, they only apply on a finite scale in a stress field where the orientation of the principal stresses (the isoclinic field) is constant. This is not the normal situation. Thus a straight slip surface as an overall failure mechanism for limit analysis, while it may be a nice guess, can seldom be exact.

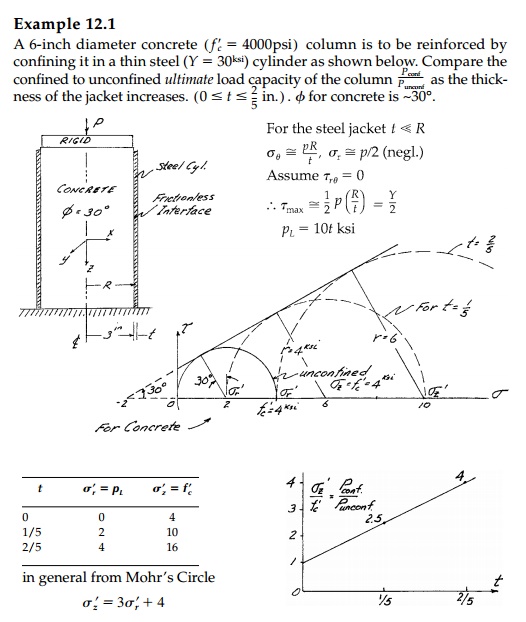
Demonstrating why, because of frictional strength, encased concrete columns are so much stronger.