SVM - Support Vector Machines

SVM—Support Vector Machines

A new classification method for both linear and nonlinear data

It uses a nonlinear mapping to transform the original training data into a higher dimension

With the new dimension, it searches for the linear optimal separating hyperplane (i.e.,

―decision boundary‖)

With an appropriate nonlinear mapping to a sufficiently high dimension, data from two classes can always be separated by a hyperplane

SVM finds this hyperplane using support vectors (―essential‖ training tuples) and margins (defined by the support vectors)

Features: training can be slow but accuracy is high owing to their ability to model complex nonlinear decision boundaries (margin maximization)

Used both for classification and prediction

Applications:

handwritten digit recognition, object recognition, speaker identification, benchmarking time-series prediction tests

1 The Case When the Data Are Linearly Separable

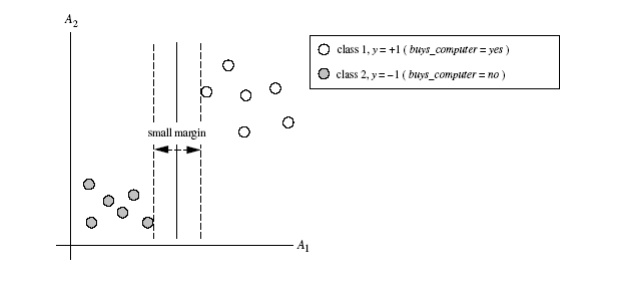
An SVM approaches this problem by searching for the maximum marginal hyperplane. Consider the below Figure , which shows two possible separating hyperplanes and their associated margins. Before we get into the definition of margins, let’s take an intuitive look at this figure. Both hyperplanes can correctly classify all of the given data tuples. Intuitively, however, we expect the hyperplane with the larger margin to be more accurate at classifying future data tuples than the hyperplane with the smaller margin. This is why (during the learning or training phase), the SVM searches for the hyperplane with the largest margin, that is, the maximum marginal hyperplane (MMH). The associated margin gives the largest separation between classes. Getting to an informal definition of margin, we can say that the shortest distance from a hyperplane to one side of its margin is equal to the shortest distance from the hyperplane to the other side of its margin, where the ―sides‖ of the margin are parallel to the hyperplane. When dealing with the MMH, this distance is, in fact, the shortest distance from the MMH to the closest training tuple of either class.

2 The Case When the Data Are Linearly Inseparable

We learned about linear SVMs for classifying linearly separable data, but what if the data are not linearly separable no straight line cajn be found that would separate the classes. The linear SVMs we studied would not be able to find a feasible solution here. Now what?

The good news is that the approach described for linear SVMs can be extended to create nonlinear SVMs for the classification of linearly inseparable data (also called nonlinearly separable data, or nonlinear data, for short). Such SVMs are capable of finding nonlinear decision boundaries (i.e., nonlinear hypersurfaces) in input space.

“So,” you may ask, “how can we extend the linear approach?” We obtain a nonlinear SVM by extending the approach for linear SVMs as follows. There are two main steps. In the first step, we transform the original input data into a higher dimensional space using a nonlinear mapping. Several common nonlinear mappings can be used in this step, as we will describe further below. Once the data have been transformed into the new higher space, the second step searches for a linear separating hyperplane in the new space.We again end up with a quadratic optimization problem that can be solved using the linear SVM formulation. The maximal marginal hyperplane found in the new space corresponds to a nonlinear separating hypersurface in the original space.