Representation of curves

Geometric models are commonly differentiated from object oriented models and procedural, which describe the shape perfectly by an opaque algorithm that creates its appearance. They are also compared with volumetric models and digital images which shows the shape as a subset of a regular partition of space; and with fractal models that provide an infinitely recursive description of the shape. Though, these differences are often fuzzy: for example, a image can be interpreted as a collection of colored squares; and geometric shape of circles are defined by implicit mathematical equations. Also, a fractal model gives a parametric model when its recursive description is truncated to a finite depth.

Representation of curves

A curve is  an  entity  related  to  a line but  which  is  not  required  to  be straight.  A  curve  is

a topological space which is internally homeomorphism to a line; this shows that a curve is a set of points which close to each of its points looks like a line, up to a deformation.

A conic  section is   a curve created   as   the  intersection  of   a cone with  a plane.  In analytic geometry,   a   conic  may   be   described   as   a plane  algebraic   curve of  degree   two,  and  as a quadric of dimension two.

There are several of added geometric definitions possible. One of the most practical, in that it involves only the plane, is that a non circular conic has those points whose distances to various point, called a ‘focus’,and several line, called a ‘directrix’,are in a fixed ratio, called the ‘eccentricity’.

1.Conic Section

Conventionally, the three kinds of conic section are the hyperbola, the ellipse and the parabola. The circle is a unique case of the ellipse, and is of adequate interest in its own right that it is sometimes described the fourth kind of conic section. The method of a conic relates to its ‘eccentricity’,those with eccentricity less than one is ellipses, those with eccentricity equal to one is parabolas, and those with eccentricity greater than one is hyperbolas. In the focus, directrix describes a conic the circle is a limiting with eccentricity zero. In modern geometry some degenerate methods, such as the combination of two lines, are integrated as conics as well.

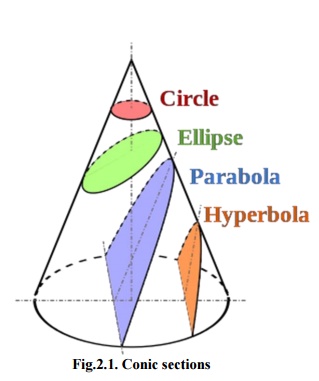
Fig.2.1. Conic sections

The three kinds of conic sections are the ellipse, parabola, and hyperbola. The circle can be taken as a fourth kind of ellipse. The circle and the ellipse occur when the intersection of plane and cone is a closed curve. The circle is generated when the cutting plane is parallel to the generating of the cone. If the cutting plane is parallel to accurately one generating line of the cone, then the conic is unbounded and is mentioned a parabola. In the other case, the figure is a hyperbola.

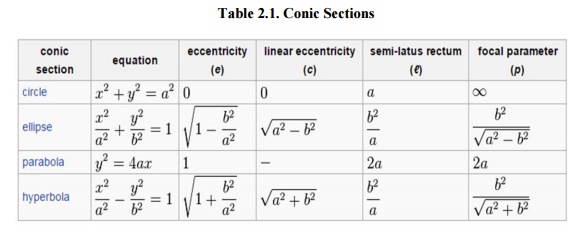
Different factors are connected with a conic section, as shown in the Table 2.1. For the ellipse, the table shows the case of ‘a’> ‘b’, for which the major axis is horizontal; for the other case, interchange the symbols ‘a’and ‘b’.For the hyperbola the east-west opening case is specified. In all cases, ‘a’nd ‘b’are positive.

Table 2.1. Conic Sections

The non-circular conic sections are accurately those curves that, for a point ‘F’,a line ‘L’not having  ‘F’and  a  number ‘e’ which  is  non-negative,  are   the locus of  points  whose   distance to ‘F’equals ‘e’ multiplies   their   distance   to ‘L’.‘F’is   called   the focus, ‘L’the   directrix, and ‘e’the eccentricity.

i. Linear eccentricity (c) is the space between the center and the focus.

ii.Latus rectum (2l) is parallel to the directrix and passing via the focus.

iii. Semi-latus rectum (l) is half the latus rectum.

iv.              Focal parameter (p) is the distance from the focus to the directrix. The relationship for the above : p*e = l and a*e=c.