Coordinate system

CO-ORDINATE SYSTEMS

A coordinate system is one which uses one or more numbers, or coordinates, to uniquely determine the position of a poi nt or other geometric element on a manifold such as Euclidean space.

Common coordinate systems are:

Number line

The simplest exam ple of a coordinate system is the identification of points on a line with real numbers using the number line. In this system, an arbitrary point O (the origin) is chosen o n a given line. The coordinate of a point P is de fined as the signed distance from O to P, where the signed distance is the distance ta ken as positive or negative dependin g on which side of the line P lies. Each point is given a unique coordinate and each real number is the coordinate of a unique point

Cartesian coordin ate system [ (x,y) and (x,y,z) ]

Polar coordinate system (ρ,θ)

Another co mmon coordinate system for the plane is the polar coordinate system. A point is chosen as the pole and a ray from this point is taken as the polar axis.

For a given angle θ, there is a single line through the pole whose angle with the polar axis is θ ( measured counter clockwise from the axis to the line). Then there is a unique point on this line whose signed distance from the or igin is r for given number r. For a gi ven pair of coordinates (r, θ) there is a single p oint, but any point is represented by many pairs of coordinates. For example (r, θ), (r, θ+2π) and (−r, θ+π) are all po lar coordinates for the same point. The pole is represented by (0, θ) for any value of θ.

Cylindrical Coord inate systems

A cylindrical coordinate system is a three-dimensional coordinate system that specifies point positions by the distance from a chos en reference axis, the direction from the axis relative to a chosen reference directio n, and the distance from a chosen reference plane perpendicular to the axis. The latter distance is given as a positive or n egative number depending on which side of t he reference plane faces the point.

The origin of the system is the point where all three coordinates can be given as zero. This is the intersection between the reference plane and the axis.

The axis is variously called the cylindrical or lon gitudinal axis, to differentiate it fro m the polar axis, which is the ray that lies in th e reference plane, starting at the origin and pointing in the reference direction.

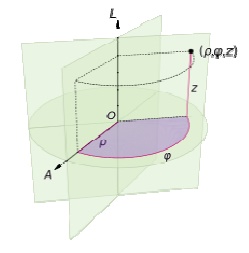
The distanc e from the axis may be called the radial distance or radius, while the angular coord inate is sometimes referred to as the angular position or as the azimuth.

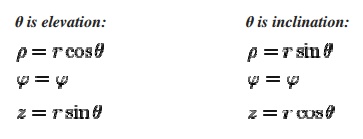
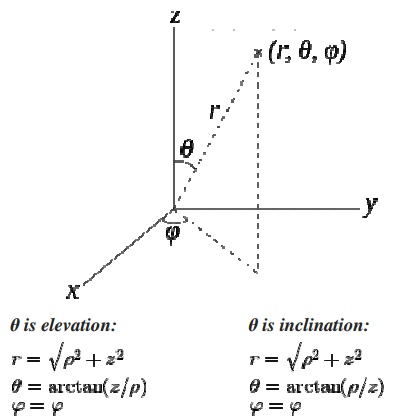
Spherical Coordi nate systems

 A spherical c oordinate system is a coordinate system for three-dimensional space where the positi on of a point is specified by three numbers: the radial distance of that point from a fixe d origin, its polar angle measured from a fixe d zenith direction, and the azimuth angl e of its orthogonal projection on a reference plane that passes through the origin an d is orthogonal to the zenith, measured from a fixed reference direction on that plane .

The radial dist ance is also called the radius or radial coordinate. The polar angle may be called co-latitu de, zenith angle, normal angle, or inclination angle

Homogeneous coo rdinate system

Three dimensional representation of a two di mensional plane is called Homogeneo us Co-ordinates. The respective system is called Homogeneous coordinate system.