Geometric Modeling

Geometric Modeling

Introduction

Geometric modeling is a part of computational geometry and applied mathematics that studies algorithms and techniques for the mathematical description of shapes.

The shapes defined in geometric modeling are generally 2D or 3D, even though several of its principles and tools can be used to sets of any finite dimension. Geometric modeling is created with computer based applications. 2D models are significant in computer technical drawing and typography. 3D models are fundamental to CAD and CAM and extensively used in many applied technical branches such as civil engineering and mechanical engineering and medical image processing.

Geometric models are commonly differentiated from object oriented models and procedural, which describe the shape perfectly by an opaque algorithm that creates its appearance. They are also compared with volumetric models and digital images which shows the shape as a subset of a regular partition of space; and with fractal models that provide an infinitely recursive description of the shape. Though, these differences are often fuzzy: for example, a image can be interpreted as a collection of colored squares; and geometric shape of circles are defined by implicit mathematical equations. Also, a fractal model gives a parametric model when its recursive description is truncated to a finite depth.

Representation of curves

A curve is  an  entity  related  to  a line but  which  is  not  required  to  be straight.  A  curve  is

a topological space which is internally homeomorphism to a line; this shows that a curve is a set of points which close to each of its points looks like a line, up to a deformation.

A conic  section is   a curve created   as   the  intersection  of   a cone with  a plane.  In analytic geometry,   a   conic  may   be   described   as   a plane  algebraic   curve of  degree   two,  and  as a quadric of dimension two.

There are several of added geometric definitions possible. One of the most practical, in that it involves only the plane, is that a non circular conic has those points whose distances to various point, called a ‘focus’,and several line, called a ‘directrix’,are in a fixed ratio, called the ‘eccentricity’.

1.Conic Section

Conventionally, the three kinds of conic section are the hyperbola, the ellipse and the parabola. The circle is a unique case of the ellipse, and is of adequate interest in its own right that it is sometimes described the fourth kind of conic section. The method of a conic relates to its ‘eccentricity’,those with eccentricity less than one is ellipses, those with eccentricity equal to one is parabolas, and those with eccentricity greater than one is hyperbolas. In the focus, directrix describes a conic the circle is a limiting with eccentricity zero. In modern geometry some degenerate methods, such as the combination of two lines, are integrated as conics as well.

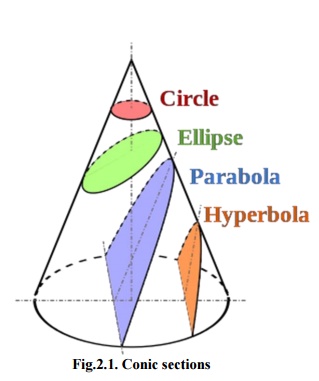
Fig.2.1. Conic sections

The three kinds of conic sections are the ellipse, parabola, and hyperbola. The circle can be taken as a fourth kind of ellipse. The circle and the ellipse occur when the intersection of plane and cone is a closed curve. The circle is generated when the cutting plane is parallel to the generating of the cone. If the cutting plane is parallel to accurately one generating line of the cone, then the conic is unbounded and is mentioned a parabola. In the other case, the figure is a hyperbola.

Different factors are connected with a conic section, as shown in the Table 2.1. For the ellipse, the table shows the case of ‘a’> ‘b’, for which the major axis is horizontal; for the other case, interchange the symbols ‘a’and ‘b’.For the hyperbola the east-west opening case is specified. In all cases, ‘a’nd ‘b’are positive.

Table 2.1. Conic Sections

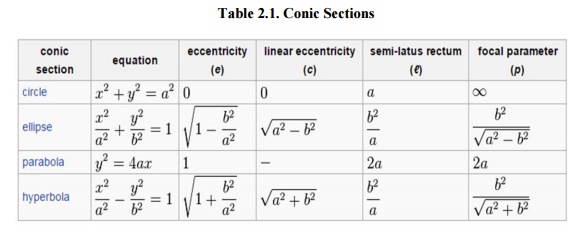
The non-circular conic sections are accurately those curves that, for a point ‘F’,a line ‘L’not having  ‘F’and  a  number ‘e’ which  is  non-negative,  are   the locus of  points  whose   distance to ‘F’equals ‘e’ multiplies   their   distance   to ‘L’.‘F’is   called   the focus, ‘L’the   directrix, and ‘e’the eccentricity.

i. Linear eccentricity (c) is the space between the center and the focus.

ii.Latus rectum (2l) is parallel to the directrix and passing via the focus.

iii. Semi-latus rectum (l) is half the latus rectum.

iv.              Focal parameter (p) is the distance from the focus to the directrix. The relationship for the above : p*e = l and a*e=c.

Hermite curve

A Hermite curve is a spline where every piece is a third degree polynomial defined in Hermite form: that is, by its values and initial derivatives at the end points of the equivalent domain interval. Cubic Hermite splines are normally used for interpolation of numeric values defined at certain dispute values x1,x2,x3, …..xn,to achieve a smooth continuous function. The data should have the preferred function value and derivative at each X_k. The Hermite formula is used to every interval (X_k,

X_k+1) individually. The resulting spline become continuous and will have first derivative.

Cubic polynomial splines are specially used in computer geometric modeling to attain curves that pass via defined points of the plane in 3D space. In these purposes, each coordinate of the plane is individually interpolated by a cubic spline function of a divided parameter‘t’.

Cubic splines can be completed to functions of different parameters, in several ways. Bicubic splines are frequently used to interpolate data on a common rectangular grid, such as pixel values in a digital picture. Bicubic surface patches, described by three bicubic splines, are an necessary tool in computer graphics. Hermite curves are simple to calculate but also more powerful. They are used to well interpolate between key points.

Fig.2.2. Hermite curve

The following vectors needs to compute a Hermite curve:

·        P1: the start point of the Hermite curve

·        T1: the tangent to the start point

·        P2: the endpoint of the Hermite curve

·        T2: the tangent to the endpoint

These four vectors are basically multiplied with four Hermite basis functions h1(s), h2(s), h3(s) and,h4(s) and added together.

h1(s) = 2s³ - 3s² + 1 h2(s) = -2s³ + 3s²

h3(s) = s³ - 2s² + s h4(s) = s³ - s²

Figure 2.3 shows the functions of Hermite Curve of the 4 functions (from left to right: h1, h2, h3, h4).

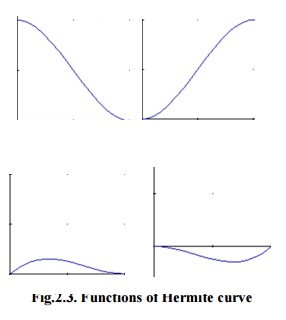
Fig.2.3. Functions of Hermite curve

A closer view at functions ‘h1’and ‘h2’,the result shows that function ‘h1’starts at one and goes slowly to zero and function ‘h2’starts at zero and goes slowly to one.

At the moment, multiply the start point with function ‘h1’and the endpoint with function ‘h2’. Let s varies from zero to one to interpolate between start and endpoint of Hermite Curve. Function

‘h3’and function ‘h4’are used to the tangents in the similar way. They make confident that the Hermite curve bends in the desired direction at the start and endpoint.

Bezier curve

Bezier curves are extensively applied in CAD to model smooth curves. As the curve is totally limited in the convex hull of its control points P0, P1,P2 & P3, the points can be graphically represented and applied to manipulate the curve logically. The control points P0 and P3 of the polygon lie on the curve (Fig.2.4.). The other two vertices described the order, derivatives and curve shape. The Bezier curve is commonly tangent to first and last vertices.

Cubic Bezier curves and Quadratic Bezier curves are very common. Higher degree Bezier curves are highly computational to evaluate. When more complex shapes are required, Bezier curves in low order are patched together to produce a composite Bezier curve. A composite Bezier curve is usually described to as a ‘path’in vector graphics standards and programs. For smoothness assurance, the control point at which two curves meet should be on the line between the two control points on both sides.

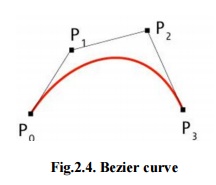
Fig.2.4. Bezier curve

A general adaptive method is recursive subdivision, in which a curve's control points are verified to view if the curve approximates a line segment to within a low tolerance. If not, the curve is further divided parametrically into two segments, 0 ≤t ≤0.5 and 0.5 ≤ ≤t1, and the same process is used recursively to each half. There are future promote differencing techniques, but more care must be taken to analyze error transmission.

Analytical methods where a Bezier is intersected with every scan line engage finding roots of cubic polynomials and having with multiple roots, so they are not often applied in practice. A Bezier curve is described by a set of control points P₀ through P_n, where ‘n’is order of curve. The initial and end control points are commonly the end points of the curve; but, the intermediate control points normally do not lie on the curve.

(i)                Linear Bezier curves

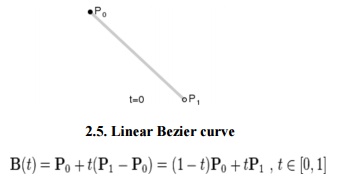
2.5. Linear Bezier curve

As shown in the figure 2.5, the given points P₀ and P₁, a linear Bezier curve is merely a straight line between those two points. The Bezier curve is represented by And it is similar to linear interpolation.

(ii) Quadratic Bezier curves

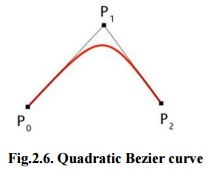
Fig.2.6. Quadratic Bezier curve

As shown in the figure 2.6, a quadratic Bezier curve is the path defined by the function B(t), given points P₀, P₁, and P₂,

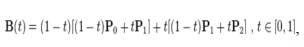
This can be interpreted as the linear interpolate of respective points on the linear Bezier curves from P₀ to P₁ and from P₁ to P₂ respectively. Reshuffle the preceding equation gives:

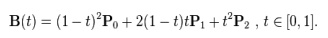
The derivative of the Bezier curve with respect to the value ‘t’is

From  which  it  can  be  finished  that  the  tangents  to  the  curve  at P₀  and P₂  intersect  at P₁.  While

‘t’increases from zero to one, the curve departs from P₀ in the direction of P₁, then turns to land at P₂ from the direction of P₁.

The following equation is a second derivative of the Bezier curve with respect to ‘t’:

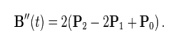
A quadratic Bezier curve is represent a  parabolic segment. Since a parabola curve is a conic section, a few sources refer to quadratic Beziers as ‘conic arcs’.

(iii) Cubic Bezier curves

As shown in figure 2.7, four control points P₀, P₁, P₂ and P₃ in the higher-dimensional space describe as a Cubic Bezier curve. The curve begins at P₀ going on the way to P₁ and reaches at P₃ coming from the direction of P₂. Typically, it will not pass through control points P₁ / P₂, these points are only there to give directional data. The distance between P₀ and P₁ determines ‘how fast’and ‘how far’the curve travels towards P₁ before turning towards P₂.

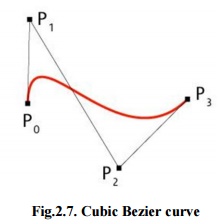
Fig.2.7. Cubic Bezier curve

The function B _{Pi, Pj, Pk} (t) for the quadratic Bezier curve written by points P_i, P_j, and P_k, the cubic Bezier curve can be described as a linear blending of two quadratic Bezier curves:

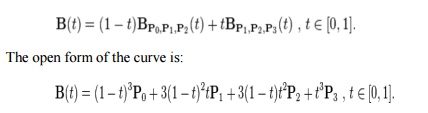
For several choices of P₁  and P₂  the Bezier curve may meet itself.

Any sequence of any four dissimilar points can be changed to a cubic Bezier curve that goes via all four points in order. Given the beginning and ending point of a few cubic Bezier curve, and the points beside the curve equivalent to t = 1/3 and t = 2/3, the control points for the original Bezier curve can be improved.

The following equation represent first derivative of the cubic Bezier curve with respect to t:

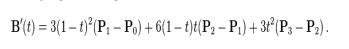
The following equation represent second derivative of the Bezier curve with respect to t:

1. Properties Bezier curve

·       The Bezier curve starts at P₀  and ends at P_n; this is known as ‘endpoint interpolation’property.

·       The Bezier curve is a straight line when all the control points of a cure are collinear.

·       The beginning of the Bezier curve is tangent to the first portion of the Bezier polygon.

·       A Bezier curve can be divided at any point into two sub curves, each of which is also a Bezier curve.

·       A few curves that look like simple, such as the circle, cannot be expressed accurately by a Bezier; via four piece cubic Bezier curve can similar a circle, with a maximum radial error of less than one part in a thousand (Fig.2.8).

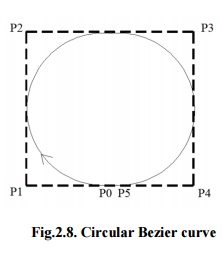
Fig.2.8. Circular Bezier curve

·       Each quadratic Bezier curve is become a cubic Bezier curve, and more commonly, each degree ‘n’Bezier curve is also a degree ‘m’curve for any m > n.

Bezier curves have the different diminishing property. A Bezier curves does not ‘ripple’more than the polygon of its control points, and may actually ‘ripple’lss than that.

·       Bezier curve is similar with respect to t and (1-t). This represents that the sequence of control points defining the curve can be changes without modify of the curve shape.

·       Bezier curve shape can be edited by either modifying one or more vertices of its polygon or by keeping the polygon unchanged or simplifying multiple coincident points at a vertex (Fig .2.19).

2. Construction of Bezier curves

(i) Linear curves:

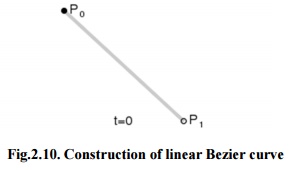
Fig.2.10. Construction of linear Bezier curve

The figure 2.10 shows the function for a linear Bezier curve can be via of as describing how far B(t) is from P₀ to P₁ with respect to ‘t’. When t equals to 0.25, B(t) is one quarter of the way from point P₀ to P₁. As ‘t’varies from 0 to 1, B(t) shows a straight line from P₀ to P₁.

(ii) Quadratic curves

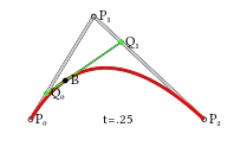
Fig.2.11. Construction of linear Quadratic curve

As  shown  in  figure  2.11,  a  quadratic  Bezier  curves  one  can  develop  by  intermediate

points Q₀ and Q₁  such that as ‘t’varies from 0 to 1:

·       Point Q₀ (t) modifying from P₀  to P₁  and expresses a linear Bezier curve.

·       Point Q₁ (t) modifying from P₁  to P₂  and expresses a linear Bezier curve.

·       Point B (t) is interpolated linearly between Q₀(t) to Q₁(t) and expresses a quadratic Bezier curve.

(iii) Higher-order curves

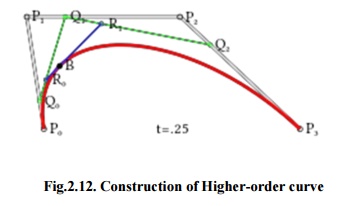
Fig.2.12. Construction of Higher-order curve

As shown in figure 2.12, a higher-order curves one requires correspondingly higher intermediate points. For create cubic curves, intermediate points Q₀, Q₁, and Q₂ that express as linear

Bezier curves, and points R₀  and R₁  that express as quadratic Bezier curves.

3. Rational Bezier curve

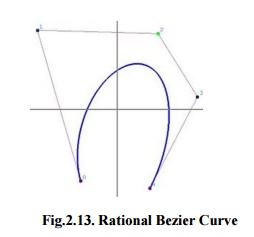
Fig.2.13. Rational Bezier Curve

The rational Bezier curve includes variable weights (w) to provide closer approximations to arbitrary shapes. For Rational Bezier Curve, the numerator is a weighted Bernstein form Bezier and the denominator is a weighted sum of Bernstein polynomials. Rational Bezier curves can be used to signify segments of conic sections accurately, including circular arcs (Fig.2.13).