Techniques In Surface Modelling

TECHNIQUES IN SURFACE MODELLING

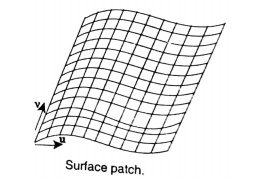
i.           Surface Patch

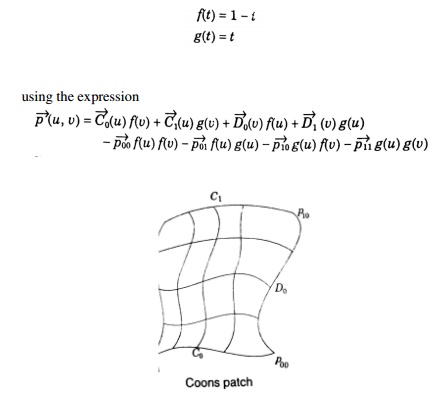
ii.           Coons Patch

iii.           Bicubic Patch

iv.          Be’zier Surface

v.           B-Spline Surface

i.           Surface Patch

The patch is the fundamental building block for surfaces. The two variables u and v vary across the patch; the patch may be termed biparametric. The parametric variables often lie in the range 0 to 1. Fixing the value of one of the parametric variables results in a curve on the patch in terms of the other variable (Isoperimetric curve). Figure shows a surface with curves at intervals of u and v of 0 : 1.

ii.  Coons Patch

The sculptured surface often involve interpolation across an intersecting mesh of curves that in effect comprise a rectangular grid of patches, each bounded by four boundary curves. The linearly blended coons patch is the simplest for interpolating between such boundary curves. This patch definition technique blends for four boundary curves Ci(u) and Dj(v) and the corner points pij of the patch with the linear blending functions,

iii.           Bicubic Patch

The bi-cubic patch is used for surface descriptions defined in terms of point and tangent vector information. The general form of the expressions for a bi-cubic patch is given by:

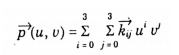
This is a vector equation with 16 unknown parameters kij which can be found by Lagrange interpolation through 4 x 4 grid.

iv.          Be’zier Surface

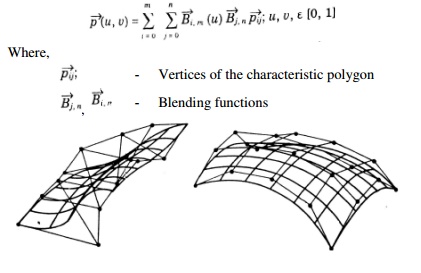
The Be’zier surface formulation use a characteristic polygon

Points the Bezier surface are given by

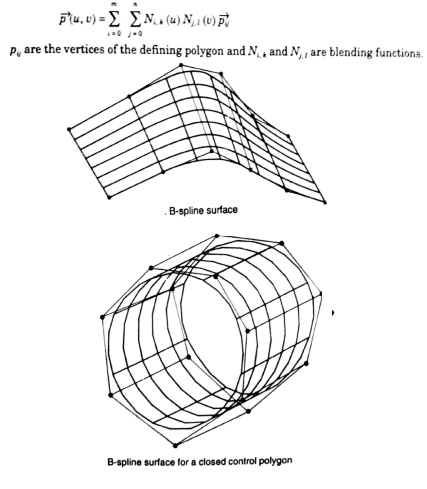
v.           B-Spline Surfaces

The B-spline surface approximates a characteristics polygon as shown and passes through the corner points of the polygon, where its edges are tangential to the edges of the polygon

This may not happen when the control polygon is closed

A control point of the surface influences the surface only over a limited portion of the parametric space of variables u and v.

The expression for the B-spline surfaces is given by