Chapter: Mechanical : Computer Aided Design : Geometric Modeling
Geometric Modeling
GEOMETRIC MODELING
PRE-REQUISITE DISCUSSION
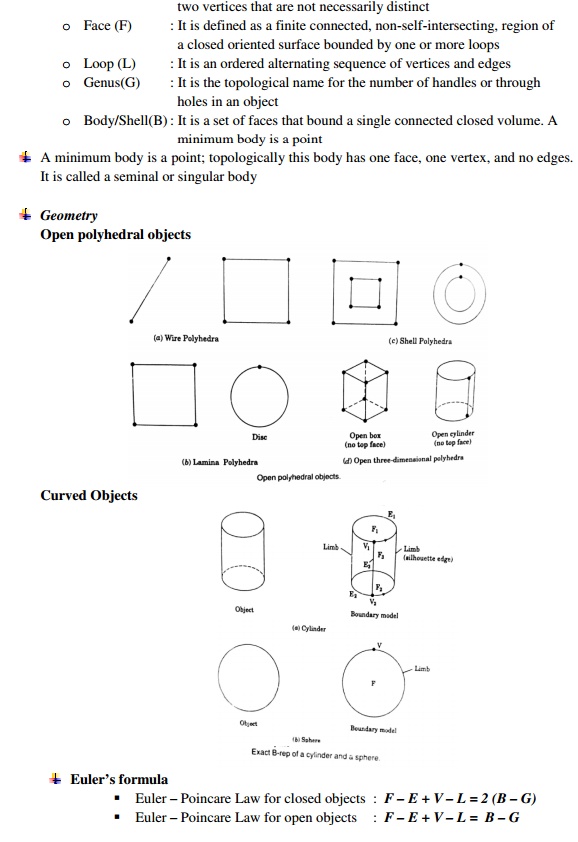
CURVE REPRESENTATION
(1) Parametric
equation x, y, z coordinates are related by a parametric var iable (u or
θ)
(2) Nonparametric
equation x, y, z coordinates are related by a function
Example: Circle (2-D)

TYPES OF CURVES USED IN GEOMETRIC MODELLING
• Hermite
curves
• Bezeir
curves
• B-spline
curves
• NURBS
curves
HERMITE CURVES

Effect of tangent vector on t he curve’s shape
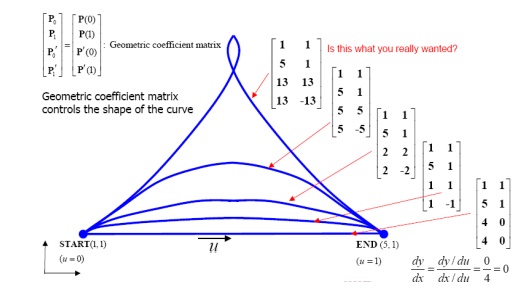
BEZIER CURVE

Two Drawbacks of Bezier Curves

B-SPLINE CURVES

NURBS curve

TECHNIQUES IN SURFACE MODELLING
i.
Surface Patch
ii.
Coons Patch
iii.
Bicubic Patch
iv.
Be’zier Surface
v.
B-Spline Surface
i.
Surface Patch
The patch is the fundamental building block for surfaces. The
two variables u and v vary across the patch; the patch may be
termed biparametric. The parametric variables often lie in the range 0
to 1. Fixing the value of one of the parametric variables results in a curve on
the patch in terms of the other variable (Isoperimetric curve). Figure
shows a surface with curves at intervals of u and v of 0 : 1.

ii. Coons Patch
The sculptured surface often
involve interpolation across an intersecting mesh of curves that in effect
comprise a rectangular grid of patches, each bounded by four boundary curves.
The linearly blended coons patch is the simplest for interpolating between such
boundary curves. This patch definition technique blends for four boundary
curves Ci(u) and Dj(v) and
the corner points pij of the patch with the linear blending
functions,
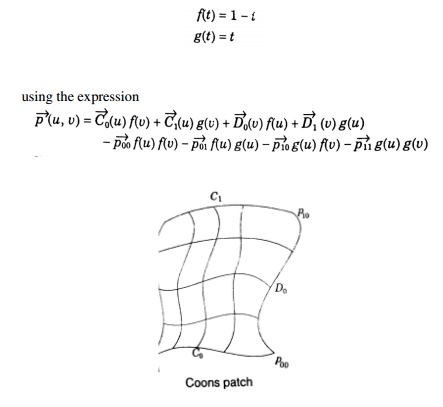
iii.
Bicubic Patch
The bi-cubic patch is used for surface
descriptions defined in terms of point and tangent vector information. The
general form of the expressions for a bi-cubic patch is given by:

This is a vector equation with 16 unknown
parameters kij which can be found by Lagrange interpolation
through 4 x 4 grid.
iv.
Be’zier Surface
The Be’zier surface formulation use
a characteristic polygon
Points the Bezier surface are given
by
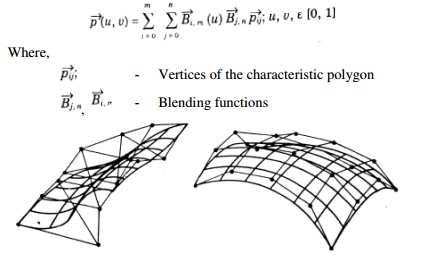
v.
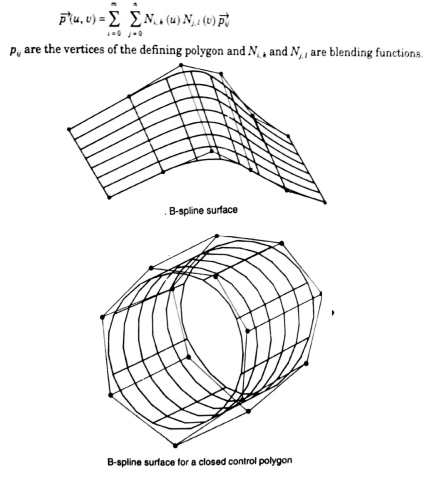
B-Spline Surfaces
The B-spline surface approximates a
characteristics polygon as shown and passes through the corner points of the
polygon, where its edges are tangential to the edges of the polygon
This may not happen when the control
polygon is closed
A control point of the surface
influences the surface only over a limited portion of the parametric space of
variables u and v.
The expression for the B-spline
surfaces is given by
GEOMETRIC MODELLING
Geometric modeling is the starting point of the
product design and manufacture process. Functions of Geometric Modeling are:
Design
Analysis
Evaluation
of area, volume, mass and inertia properties
Interference
checking in assemblies
Analysis
of tolerance build-up in assemblies
Kinematic
analysis of mechanisms and robots
Automatic
mesh generation for finite element analysis
Drafting
Automatic
planar cross-sectioning
Automatic
hidden lines and surface removal
Automatic
production of shaded images
Automatic
dimensioning
Automatic
creation of exploded views of assemblies
Manufacturing
Parts
classification
Process
planning
NC data
generation and verification
Robot
program generation
Production
Engineering
Bill of
materials
Material requirement
Manufacturing
resource requirement
Scheduling
Inspection
and quality control
Program
generation for inspection machines
Comparison
of produced parts with design
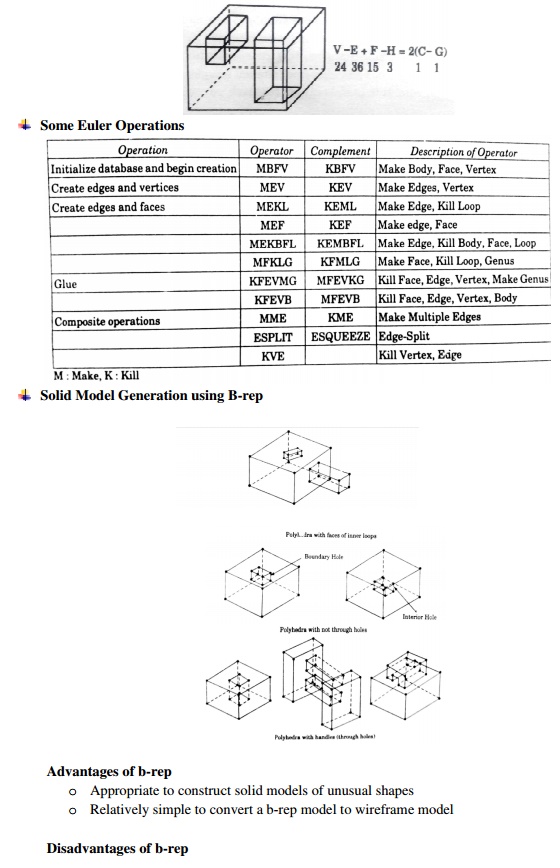
PROPERTIES OF A GEOMETRIC MODELING SYSTEM
The geometric model must stay
invariant with regard to its location and orientation The solid must have an
interior and must not have isolated parts
The solid must be finite and occupy only a finite shape
The application of a
transformation or Boolean operation must produce another solid The solid must
have a finite number of surfaces which can be described
The boundary of the solid must not be ambiguous
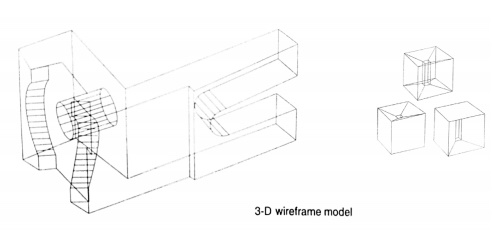
WIRE FRAME MODELING
It uses networks of
interconnected lines (wires) to represent the edges of the physical objects
being modeled
Also called ‘Edge-vertex’ or ‘stick-figure’ models Two types
of wire frame modeling:
1. 2 ½ - D
modeling
2. 3 – D
modeling
3-D Wire frame models: These are
Simple and easy to create, and
they require relatively little computer time and memory; however they do not
give a complete description of the part. They contain little information about
the surface and volume of the part and cannot distinguish the inside from the
outside of part surfaces. They are visually ambiguous as the model can be interpreted
in many different ways because in many wire frame models hidden lines cannot be
removed. Section property and mass calculations are impossible, since the
object has no faces attached to it. It has limited values a basis for
manufacture and analysis
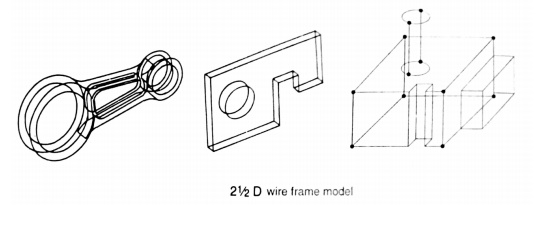
2 ½ - D Wire frame models:
Two classes of shape for which a
simple wire-frame representation is often adequate are those shapes defined by
projecting a plane profile along its normal or by rotating a planar profile
about an axis. Such shapes are not two-dimensional, but neither do they require
sophisticated three-dimensional schemes for their representation. Such
representation is called 2 ½ - D.


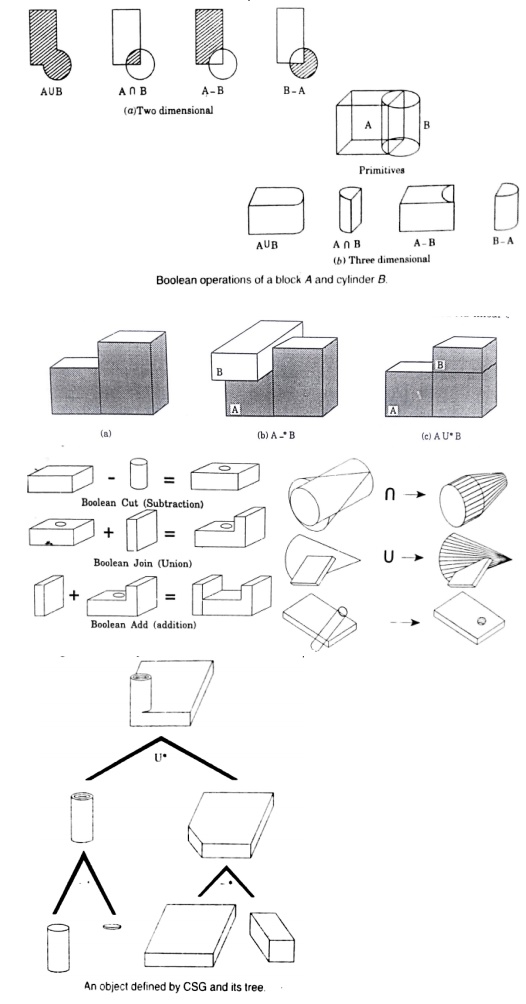
Related Topics