Relating Abortive Initiations to Binding and Initiating

Relating Abortive Initiations to Binding and Initiating

The binding and initiation reactions explained in the previous section are described by the following equation:

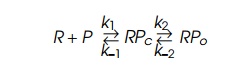
where R is RNA polymerase free in solution, P is uncomplexed promoter RP_c is promoter with RNA polymerase bound in an inactive state definedas “closed,” and RP₀ is promoter with RNA polymerase bound in an active state called “open” because it can immediately begin transcrip-tion if provided nucleotides.

If RNA polymerase and DNA containing a promoter are mixed together, then the concentration of RP₀ at all times thereafter can be calculated in terms of the initial concentrations R and P and the four rate constants; however, the resulting solution is too complex to be of much use. A reasonably close mathematical description of the actual situation can be found by making three approximations. The first is that R be much greater than P_o. This is easily accomplished because theconcentrations of R and P added are under the experimentalist’s control. The second is known to enzymologists as the steady-state assumption. Frequently the rate constants describing reactions of the type written above are such that, during times of interest, the rate of change in the amount of RP_c, is small, and the amount of RP_c can be considered to be in equilibrium with R, P, and RP_c. That is,

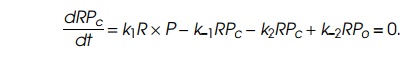
The third assumption is that k_-2 is much smaller than k₂. Experiments show this to be a very good approximation. RNA polymerase frequently takes hours or days to dissociate from a promoter. Straightforward solution of the equations then yields RP_o as a function of time in a useful form:

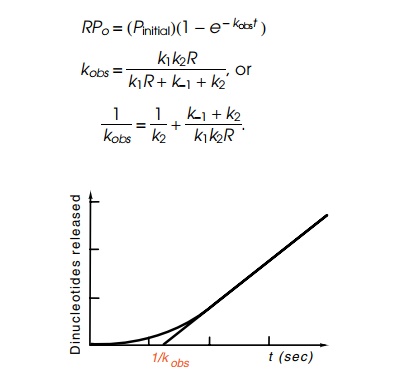
Figure 4.20 Determination of theparameter kobs from the kinetics of incorporation of radioactivity into dinucleotides

After starting the binding initiation assay, the total amount of oli-gonucleotides synthesized by any time can be measured by removing a sample from the synthesis mixture and chromatographically separating nucleoside triphosphates from the short oligonucleotides. Since the rate of oligonucleotide production is proportional to RP₀, the total amount of oligonucleotides synthesized as a function of time is given by

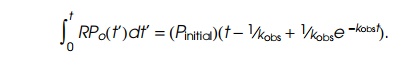
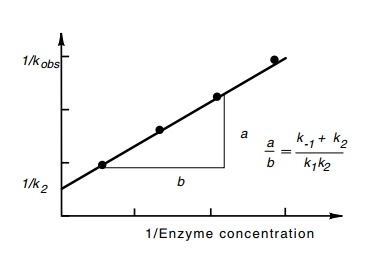
At very large t this increases linearly as P_initial(t−¹⁄k_obs). Hence extrapo-lating the linear portion of the curve to the point of zero oligonucleotides gives 1/k_obs (Fig. 4.20). As seen above, 1/k_obs in the limit of high R yields 1/k₂. At other concentrations, (k_-1 + k₂/k₁k₂) is a linear function of 1/R. Performing the abortive initiation reaction at a variety of concentrations of R and measuring the kinetics of synthesis of oligonucleotides permits straightforward evaluation of k₂ (Fig. 4.21). Often, k_-1 is much greater than k₂, in which case the ratio k₁/k_-1, called K_B, or equivalently, k_-1/k₁ which is called K_d, is obtained as well.

Figure 4.21 Determination of the kinetic parameters describing initiation byDNA polymerase from a series of kobs values obtained at different RNA polym-erase concentrations. 

A variety of promoters have been examined by these techniques. Highly active promoters must bind polymerase well and must perform the initiation “isomerization” quickly. Less active promoters are poor in binding RNA polymerase or slow in isomerization.