Chapter: Programming and Data structures : Advanced Non-Linear Data Structures
Red–black tree
RED-BLACK
TREES
A
red–black tree is a data
structure which is a
type of self-balancing binary
search tree.
Balance
is preserved by painting each node of the tree with one of two colors
(typically called 'red' and 'black') in a way that satisfies certain
properties, which collectively constrain how unbalanced the tree can become in
the worst case. When the tree is modified, the new tree is subsequently
rearranged and repainted to restore the coloring properties. The properties are
designed in such a way that this rearranging and recoloring can be performed
efficiently.
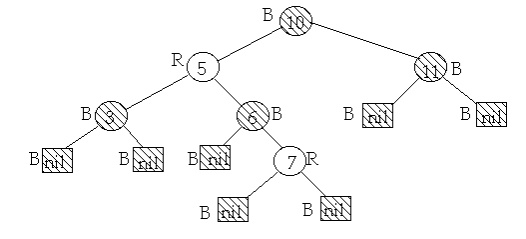
A binary
search tree is a red-black tree if:
1. Every
node is either red or black
2. Every
leaf (nil) is black
3. If a node
is red, then both its children are black
4. Every
simple path from a node to a descendant leaf contains the same number of black
nodes
Black-height
of a node x, bh(x), is the number of black nodes on any path from x to a leaf,
not counting x
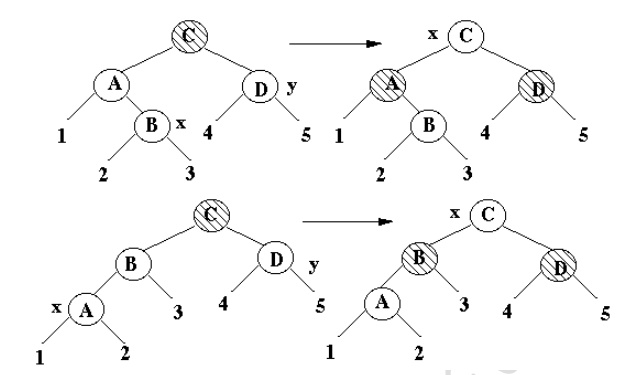
Inserting in Red-Black Tree
·
Color the node Red
·
Insert as in a regular BST
·
If have parent is red
Case 1
·
x is node of interest, x's uncle is Red
· Decrease x's black height by one
Case 2
·
x's uncle is Black, x is a Right child
·
Transform to case 3
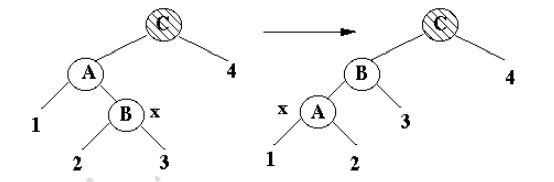
Case 3
·
x's uncle is Black, x is a Left child
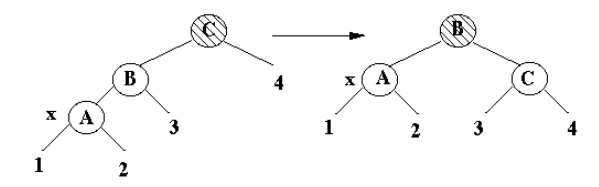
·
Terminal case, tree is Red-Black tree
·
Insertion takes O(lg(n)) time
·
Requires at most two rotations
Example:
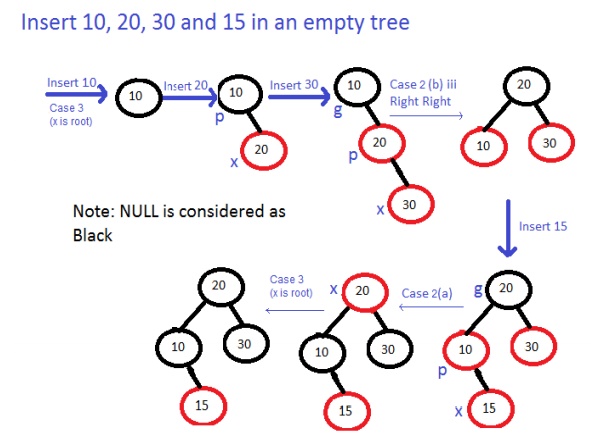
Deleting in a Red-Black Tree
·
Find node to delete
·
Delete node as in a regular BST
·
Node to be deleted will have at most one child
·
If we delete a Red node tree still is a Red-Black
tree
·
Assume we delete a black node
·
Let x be the child of deleted node
·
If x is red, color it black and stop
·
If x is black mark it double black and apply the
following:
Case 1
·
x's sibling is red
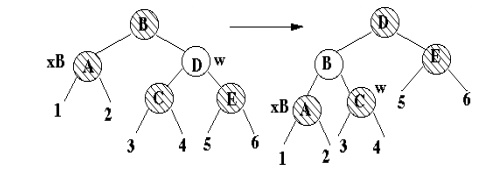
·
x stays at same black height. Transforms to case 2b
then terminates.
Case 2a
·
x's sibling is black
·
x's parent is black
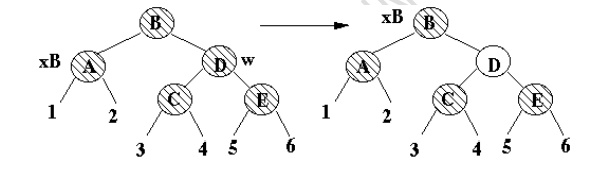
·
Decreases x black height by one
Case 2b
·
x's sibling is black
·
x's parent is red
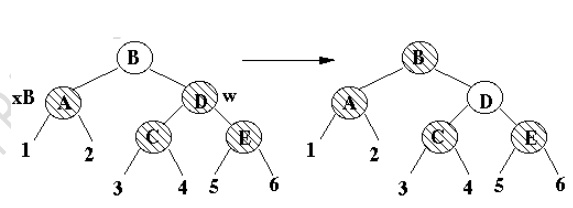
Terminal
case, tree is Red-Black treep
Case 3
·
x's sibling is black
·
x's parent is either
·
x's sibling's left child is red
·
x's sibling's right child is black
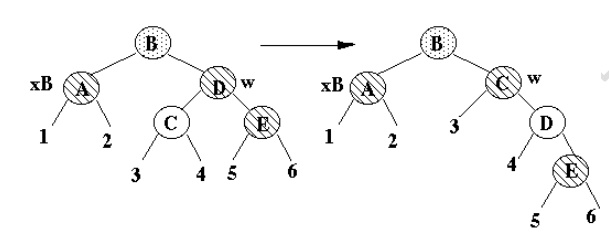
· x stays at same black height
·
Transforms to case 4
Case 4
·
x's sibling is black
·
x's parent is either
·
x's sibling's left child is either
·
x's sibling's right child is red
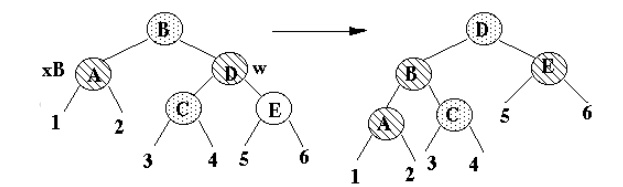
·
Terminal case, tree is Red-Black tree.
·
Delete time is O(lg(n)).
·
At most three rotations are done.
Related Topics