Quartile Deviation

Quartile Deviation

Quartile Deviation is defined as QD = ½ (Q₃ – Q₁) It may also be called as semi- inter quartile.

where Q₁ and Q₃ are the first and third quartiles of the distribution respectively and Q₃ – Q₁ is called as inter quartile range.

(i) Relative measures for QD

Quartile deviation is an absolute measure of dispersion. The relative measure corresponding to this measure, called the coefficient of quartile deviation is calculated as follows:

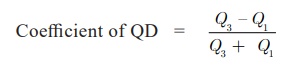
Coefficient of quartile deviation can be used to compare the degree of variation in different distributions.

(ii) Computation of Quartile Deviation

The process of computing quartile deviation is very simple since we just have to compute the values of the upper and lower quartiles that is Q₃ and Q₁ respectively.

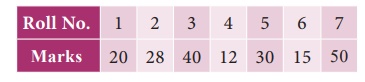
Example 8.16

Calculate the value of quartile deviation and its coefficient from the following data

Solution :

Marks are arranged in ascending order

Hence coefficient of QD = 0.455

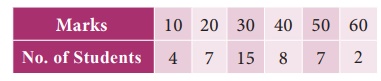
Example 8.17

Compute coefficient of quartile deviation from the following data

Solution :

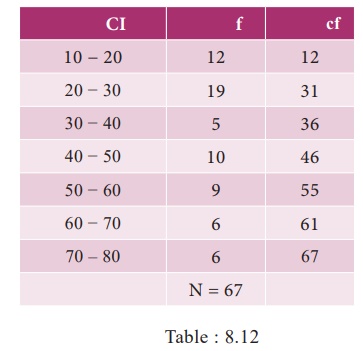
Example 8.18

Compute Quartile deviation from the following data

Solution :