Harmonic mean

Harmonic mean

Harmonic mean is defined as the reciprocal of the arithmetic mean of the reciprocal of the individual observations. It is denoted by HM

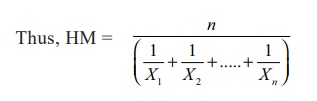
When the number of items is large the computation of harmonic mean in the above manner becomes tedious. To simplify calculations we obtain reciprocals of the various items from the tables and apply the following formulae:

(i) In individual observations

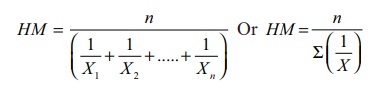
where n is number of observations or items or values

(ii)  In discrete frequency distribution

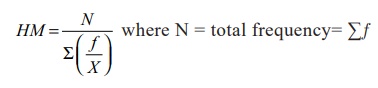
(iii) In continuous frequency distribution

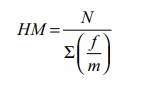
Where m is midpoint and N is total frequency

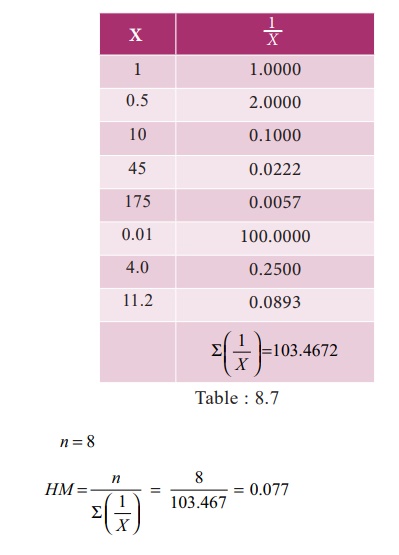
Example 8.9

Calculate the Harmonic Mean of the following values:

1, 0.5, 10, 45.0, 175.0, 0.01, 4.0, 11.2

Solution:

Example 8.10

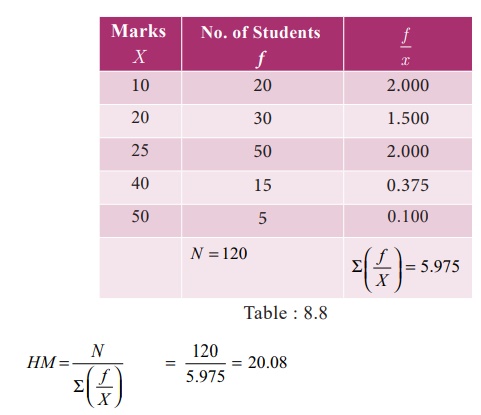
From the following data compute the value of Harmonic Mean .

Solution:

Calculation of Harmonic Mean

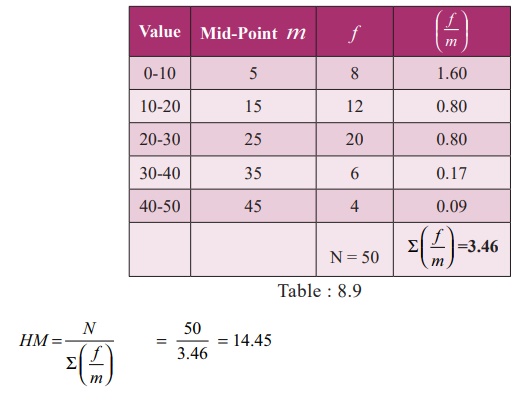
Example 8.11

Calculate Harmonic Mean for the following data given below

Solution:

Calculation of Harmonic Mean

Special applications of Harmonic Mean

The Harmonic Mean is restricted in its field of usefulness. It is useful for computing the average rate of increase of profits of a concern or average speed at which a journey has been performed or the average price at which an article has been sold. The rate usually indicates the relation between two different types of measuring units that can be expressed reciprocally.

For example, if a man walked 20km in 5 hours, the rate of his walking speed can be expressed

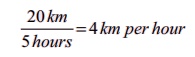
where the units of the first term is a km and the unit of the second term is an hour or reciprocally,

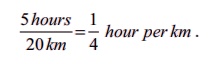
where the unit of the first term is an hour and the unit of the second term is a km

Example 8.12

An automobile driver travels from plain to hill station 100km distance at an average speed of 30km per hour. He then makes the return trip at average speed of 20km per hour what is his average speed over the entire distance (200km)?

Solution:

If the problem is given to a layman he is most likely to compute the arithmetic mean of two speeds

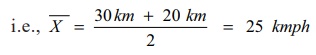
But this is not the correct average.

So harmonic mean would be mean suitable in this situation. Harmonic Mean of 30 and 20 is

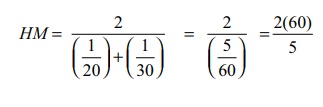
NOTE

The Harmonic Mean is a measure of central tendency for data expressed as rates such as kilometres per hour, kilometres per litre, periods per semester, tonnes per month etc.,