Conditional Probability

Conditional Probability

If two events A and B are dependent, then the conditional probability of B given that A as occurred already is

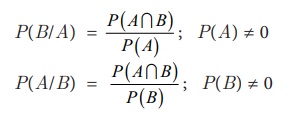
(i) Multiplication Theorem:

The probability of the simultaneous happening of two events A and B is given by

P(A∩B) = P(A).P(B/A) or

P(A∩B) = P(B).P(A/B)

NOTE

If A and B are two independent events then        P(A and B) = P(A∩B) = P(A) P(B)

The theorem can be extended to three or more independent events. Thus for three events the theorem states that

P(A and B and C) = P (A∩B∩C) = P(A) P(B) P(C)

Example 8.24

An unbiased die is thrown. If A is the event ‘the number appearing is a multiple of 3’ and B be the event ‘the number appearing is even’ number then find whether A and B are independent?

Solution:

We know that the sample space is S = {1,2,3,4,5,6}

Now, A = {3,6} ; B = { 2,4,6} then (A∩B) ={6}

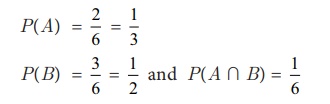
Clearly P(A ∩ B) = P(A) P(B)

Hence A and B are independent events.

Example 8.25

Let P(A) = 3/5 and P(B) = 1/5. Find P(A ∩ B) if A and B are independent events.

Solution:

Since A and B are independent events then P(A∩B) = P(A) P(B)

Example 8.26

Three coins are tossed simultaneously. Consider the events A ‘three heads or three tails’, B ‘atleast two heads’ and C ‘at most two heads’ of the pairs (A,B), (A,C) and (B,C), which are independent? Which are dependent?

Solution:

Here the sample space of the experiment is

S= {HHH, HHT, HTH, HTT, THH, TTH, THT, TTT}

A = {Three heads or Three tails} ={HHH, TTT}

B = {at least two heads} ={HHH, HHT, HTH, THH}

And C = {at most two heads} = {HHT, HTH, HTT, THH, TTH, THT, TTT}

Also (A∩B) = {HHH}; (A∩C) = {TTT} and (B∩C) ={HHT, HTH, THH}

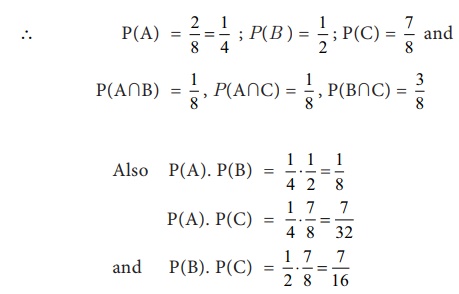
Thus, P(A∩B) = P(A). P(B)

 P(A∩C) ≠ P(A) . P(C) and

 P(B∩C) ≠ P(B). P(C)

Hence, the events (A and B) are independent, and the events (A and C) and (B and C) are dependent.

Example 8.27

A can solve 90 per cent of the problems given in a book and B can solve 70 per cent. What is the probability that at least one of them will solve a problem selected at random?

Solution:

Given the probability that A will be able to solve the problem

Hence the probability that at least one of them will solve the problem =  97/100

Example 8.28

A bag contains 5 white and 3 black balls. Two balls are drawn at random one after the other without replacement. Find the probability that both balls drawn are black.

Solution:

Let A, B be the events of getting a black ball in the first and second draw Probability of drawing a black ball in the first attempt is

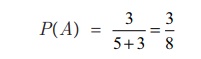
Probability of drawing the second black ball given that the first ball drawn is black

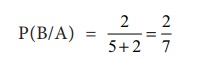
∴ The probability that both balls drawn are black is given by

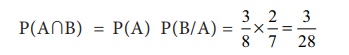
Example 8.29

In a shooting test the probability of hitting the target are ¾ for A, ½ for B and 2/3 for C. If all of them fire at the same target, calculate the probabilities that

(i) All the three hit the target

(ii) Only one of them hits the target

(iii) At least one of them hits the target

Solution:

Example 8.30

Find the probability of drawing a queen, a king and a knave (Jack) in that order from a pack of cards in three consecutive draws, the card drawn not being replaced.

Solution :

Let

A : the card drawn is a queen

B: the card drawn is a king

C: the card is drawn is a knave(jack)

P(drawing a queen card) =