Average

Average

- Recall

There are several measures of central tendency for the data. They are

·        Arithmetic Mean

·        Median

·        Mode

·        Geometric Mean

·         Harmonic Mean

Arithmetic Mean (discrete case)

Arithmetic mean of a set of observations is their sum divided by the number of observations. The observation are classified into a) Ungrouped data and b) Grouped data.

a) Ungrouped data

(i)      Direct Method:

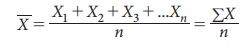
where is Arithmetic Mean, ∑X is sum of all the values of the variable X and n is number of observations.

(ii)  Short-cut method

The arithmetic mean can be calculated by using any arbitrary value A as origin and write d as the deviation of the variable X then,

b) Grouped data

Direct method

The formula for computing the mean is

where f is frequency; X is the variable; N = ∑ f i.e. total frequency.

(ii)  Short-cut method

The arithmetic mean is computed by applying the following formula:

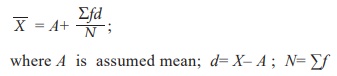
Arithmetic mean for Continuous case

The arithmetic mean may be computed by applying any of the following methods:

(i) Direct method

(ii) Short-cut method

(iii) Step deviation method

(i) Direct method

When direct method is used arithmetic mean is defined as

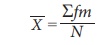
Where m = midpoint of each of the class interval,

f = the frequency of each class interval

N = ∑f = total frequency

(iii) Short-cut method

The arithmetic mean is computed by applying the following formula

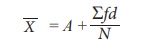
where A is assumed mean or arbitrary value, d=m–A is deviations of mid-point from assumed mean and N=∑f

(iii) Step Deviation Method

In case of grouped or continuous frequency distribution, the arithmetic mean

is any arbitrary value or assumed mean and c is the magnitude of class interval.

Mode:

Mode is the value which repeats maximum number of times among the given observations.

Median:

Median is exactly a middle value and it exceeds and exceeded by the same number of observations. Median is one of the positional measure. Some other related positional measures are also described below.