Basic concepts of Probability

Basic concepts of Probability

Recall

(i) Random Experiment

If an experiment or trial can be repeated under the same conditions, any number of times and it is possible to count the total number of outcomes, but individual result ie., individual outcome is not predictable, then the experiment is known as random experiment.

Example: Tossing a coin, throwing a die, selecting a card from a pack of playing cards, etc.

(ii) Outcome:

The result of a random experiment will be called an outcome.

(iii) Trial and Event:

Any particular performance of a random experiment is called a trial and outcome or combinations of outcomes are termed as events.

(iv)  Exhaustive Events:

The total number of possible outcomes of a random experiment is known as the exhaustive events.

(v) Favourable Events:

The number of cases favourable to an event in a trial is the number of outcomes which entail the happening of the event.

(vi) Mutually Exclusive events:

Events are said to be mutually exclusive if the happening of any one of them precludes the happening of all the others, ie., if no two or more of them can happen simultaneously in the same trial. Symbolically the event A and B are mutually exclusive if A ∩ B = ∅ .

(vii) Equally Likely Events:

Events (two or more) of an experiment are said to be equally likely, if any one of them cannot be expected to occur in preference to the others.

(viii) Classical definition of Probability

If a random experiment or trial results in ‘n’ exhaustive, mutually exclusive and equally likely outcomes (or cases), out of which m are favourable to the occurrence of an event E, then the probability ‘p’ of occurrence (or happening) of E, usually denoted by P(E), is given by

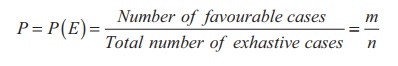
Properties

(i) 0≤P(E)≤1

(ii) Sum of all the probability equal to 1.

(iii) If P(E)=0 then E is an impossible event.

For example : A coin is tossed. Find the probability of getting a head

Solution: The total possible outcomes of an experiment {H,T}

Therefore n = 2

The favourable outcome for getting a head {H}. Therefore m =1. Thus the required probability is

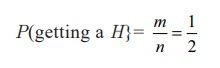
(x) Modern Definition of Probability

The modern approach to probability is purely axiomatic and it is based on the set theory concepts. In order to study, the theory of probability with an axiomatic approach it is necessary to define certain basic concepts. They are

(i) Sample Space: Each possible outcome of an experiment that can be repeated under similar or identical conditions is called a sample point and the collection of sample points is called the sample space, denoted by S.

(ii) Event: Any subset of a sample space is called an event.

(iii) Mutually Exclusive events:  Two events A and B are said to be mutually exclusive events if A ∩ B = Ï• i.e., if A and B are disjoint sets.

Example: Consider        S       = { 1,2,3,4,5}

Let     A = the set of odd numbers     = {1,3,5}

and    B = the set of even numbers    = {2,4}

Then           A∩B = Ï•

Therefore the events A and B are mutually exclusive

(xi) Observation:

Statement meaning in terms of Set theory approach

(xii) Definition of Probability (Axiomatic approach)

Let E be an experiment. Let S be a sample space associated with E. With every event in S we associate a real number denoted by P(A) called the probability of the event A satisfying the following axioms.

Axiom 1 :  P(A)≥0

Axiom 2 :  P(S)=1

Axiom 3     :  If A₁ , A₂ ,......, A_n  be a sequence of n mutually exclusive events in then

P ( A₁ UA₂U…UA_n ) = P ( A₁ )+ P ( A₂ )+ …+ P ( A_n )

(xiii) Basic Theorems on probability

Theorem 1:

Then P( ∅ ) = 0 i.e., probability of an impossible event is zero.

Theorem 2:

Let S be the sample space and A be an event in S then P(  ) ≡ 1– P(A)

Theorem 3: Addition Theorem

If A and B are any two events then P ( A ∪ B ) = P( A ) + P( B ) − P( A ∩ B)

(xiv) Observation:

(i) If the two events A and B are mutually exclusive then A∩B = ∅

∴P(A∩B) = 0

⇒P(AUB) = P(A) + P(B)

(ii) The addition theorem may be extended to any three events A,B,C and we have

P ( A∪ B ∪ C) = P ( A) + P ( B)+ P ( C) − P ( A∩ B ) − P( A ∩ C) − P ( B ∩ C) + P ( A∩ B∩C)

It is believed that the students might be familiar with the above concepts and our present syllabus continues from the following.