Probability - BayeŌĆÖs Theorem | 11th Business Mathematics and Statistics(EMS) : Chapter 8 : Descriptive statistics and probability
Chapter: 11th Business Mathematics and Statistics(EMS) : Chapter 8 : Descriptive statistics and probability
BayeŌĆÖs Theorem
BayeŌĆÖs Theorem
If E1 , E2 , E3 ..., En are a set of n mutually exclusive and collectively exhaustive events with P(Ei) ŌēĀ 0 (i = 1,2,3ŌĆ”, n), then for any arbitrary event A which is associated with sample space S = Ui=1n Ei such that P(A) > 0, we have
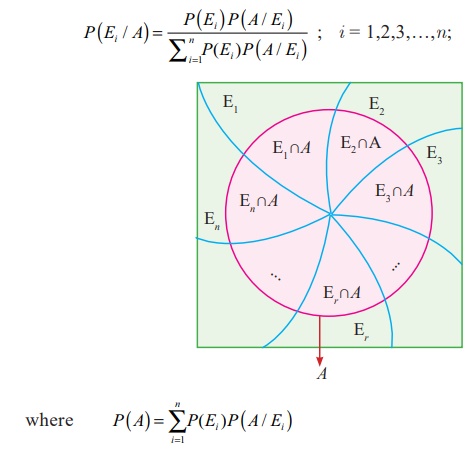
Example 8.31
Bag I
contains 3 red and 4 blue balls while another Bag II contains 5 red and 6 blue
balls. One ball is drawn at random from one of the bags and it is found to be
red. Find the probability that it was drawn from second Bag.
Solution
Let E1 be the event of choosing
the first bag, E2 the
event of choosing the second bag and A
be the events of drawing a red ball. Then P(E1) = P(E2) = ┬Į
Also P(A/E1)
= P(drawing a red ball from Bag I) = 3/ 7
And P(A/E2)
= P(drawing a red ball from Bag II) = 5 /11
Now, the
probability of drawing a ball from Bag II, being given that it is red, is P(E2/A).
By using
BayeŌĆÖs theorem, we have

Example 8.32
X speaks truth 4 out of 5 times. A
die is thrown. He reports that there is a six. What is the chance that actually there was a six?
Solution:
Let us define the following
events.
E1 : X speaks truth;
E2 : X tells a lie;
E : X reports a six;
From the
data given in the problem, we have
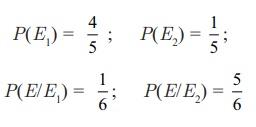
The
required probability that actually there was six (by Bayes theorem) is P(E1)
P(E/E1)
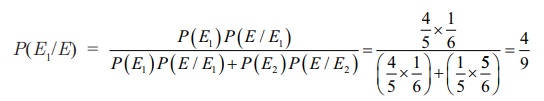
P(E1)
P(E/E1)+ P(E2) P(E/E2)
Example 8.33
A factory
has 3 machines A1, A2, A3 producing 1000, 2000, 3000 screws per day
respectively. A1 produces
1% defectives, A2 produces
1.5% and A3 produces 2%
defectives. A screw is chosen at random at the end of a day and found
defective. What is the probability that it comes from machines A1?
Solution:

Let B be
the event that the chosen screw is defective
Ōł┤P(B/A1)
= P(that defective screw from the machine
A1) = 0.01
P(B/A2) = P(that
defective screw from the machine A2)
= 0.015 and
P(B/A3) = P(that
defective screw from the machine A3)
= 0.02
We have
to find P(A1/B)
Hence by
BayeŌĆÖs theorem, we get

Exercise 8.2
1. A
family has two children. What is the probability that both the children are
girls given that at least one of them is a girl?
2. A die
is thrown twice and the sum of the number appearing is observed to be 6. What
is the conditional probability that the number 4 has appeared at least once?
3. An
unbiased die is thrown twice. Let the event A
be odd number on the first throw and B
the event odd number on the second throw. Check whether A and B events are
independent.
4. Probability of solving
specific problem independently by A
and B are ┬Į and 1/3
respectively. If both try to solve the
problem independently, find the probability that the problem is
(i) solved
(ii) exactly
one of them solves the problem
5. Suppose
one person is selected at random from a group of 100 persons are given in the
following
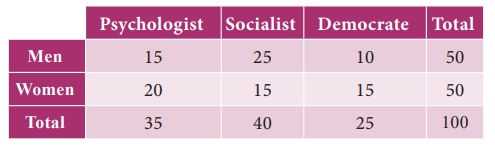
What is the probability that the
man selected is a Psychologist?
6. Two
urns contains the set of balls as given in the following table
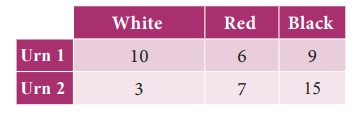
One ball is drawn from each urn
and find the probability that
(i) both balls are red
(ii) both balls are of the same colour.
7. Bag I contains 3 Red and 4 Black balls while
another Bag II contains 5 Red and 6 Black balls. One ball is drawn at random
from one of the bags and it is found to be red. Find the probability that it
was drawn from Bag I.
8. The
first of three urns contains 7 White and 10 Black balls, the second contains 5
White and 12 Black balls and third contains 17 White balls and no Black ball. A
person chooses an urn at random and draws a ball from it. And the ball is found
to be White. Find the probabilities that the ball comes from
(i) the first urn
(ii) the second urn
(iii) the third urn
9. Three
boxes B1 , B2 , B3 contain lamp bulbs some of which are defective. The
defective proportions in box B1, box B2 and box B3 are respectively 1/2 , 1/8
and 3/4 . A box is selected at random and a bulb drawn from it. If the selected
bulb is found to be defective, what is the probability that box B1 was selected?
10. Three
horses A, B, C are in race. A is twice as likely to win as B and B is twice as
likely to win as C. What are their respective probabilities of winning?
11. A die
is thrown. Find the probability of getting
(i) a
prime number
(ii) a number
greater than or equal to 3
12. Ten
cards numbered 1 to 10 are placed in a box, mixed up thoroughly and then one
card is drawn randomly. If it is known that the number on the drawn card is
more than 4. What is the probability that it is an even number?
13. There
are 1000 students in a school out of which 450 are girls. It is known that out
of 450, 20% of the girls studying in class XI. A student is randomly selected
from 1000 students. What is the probability that the selected student is from
class XI given that the selected student is a girl?
14. From
a pack of 52 cards, two cards are drawn at random. Find the probability that
one is a king and the other is a queen.
15. A
card is drawn from a pack of playing cards and then another card is drawn
without the first being replaced. What is the probability of drawing
(i) two
aces
(ii) two
spades
16. A
company has three machines A, B, C which produces 20%, 30% and 50% of the
product respectively. Their respective defective percentages are 7, 3 and 5.
From these products one is chosen and inspected. If it is defective what is the
probability that it has been made by machine C?
Related Topics