Mean deviation

Mean deviation

Mean Deviation (MD) is defined as the average of the absolute difference between the items in a distribution and the mean or median of that series.

(i) Computation of Mean Deviation - Individual observations

If X ₁ , X₂ , X ₃ ,...X_n are n given observation then the mean deviation about mean or median is as follows

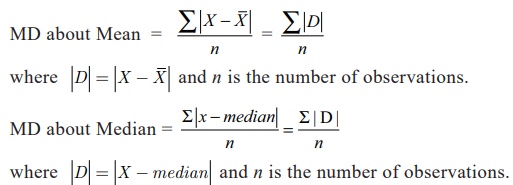
NOTE

If the Mean deviation is computed from Median then in that case D shall denote deviations of the items from Median, ignoring signs.

(ii) Computation of Mean Deviation - Discrete series

In discrete series the formula for calculating mean deviation is

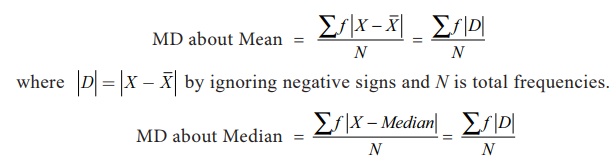
where |D| = |X – Median| by ignoring negative sign and N is total frequencies.

(iii) Calculation of Mean Deviation- Continuous Series

For calculating Mean deviation in continuous series we have to obtain the midpoints of the various classes and take the deviations of these mid points from mean or median.

where M is a mid value, |D| = |M–Median| (by ignoring negative sign) and N is the total frequencies.

(iv) Relative Measure for Mean Deviation

The relative measure corresponding to the mean deviation is called the coefficient of mean deviation and it is obtained as follows

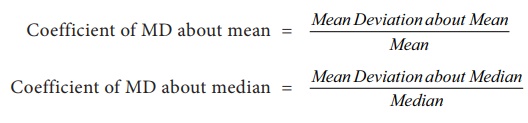
NOTE

However, in practice the arithmetic mean is more frequently used in calculating the mean deviation. If specifically stated to calculate mean deviation about median, median can be used.

Example 8.19

Calculate the Mean Deviation about mean and its coefficient of the income groups of five, given below

Solution:

Calculation of Mean Deviation about Mean

Example 8.20

Calculate the mean deviation about median and its relative measure for seven numbers given below: 55, 45, 40, 20, 60, 80, and 30.

Solution:

Arrange the values in ascending order 20, 30, 40, 45, 55, 60, 80

Example 8.21

Calculate the Mean deviation about mean for the following data.

Solution:

Calculation of Mean Deviation about Mean

Example 8.22

Calculate the Mean deviation about median and its relative measure for the following data.

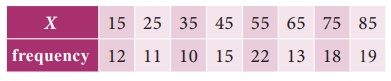
Solution:

Already the values are arranged in ascending order then Median is obtained by the following

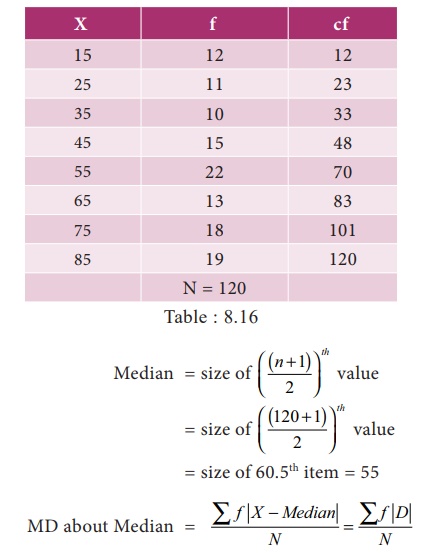
Mean deviation about Median

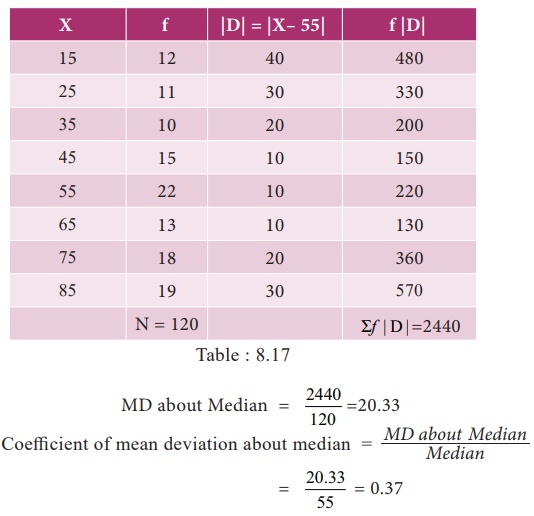
Example 8.23

Find out the coefficient of mean deviation about median in the following series

Calculations have to be made correct to two places of decimals.

Solution:

Calculation for median follows by the following table

N/2 = 212 / 2 = =106. Class interval corresponding to cumulative frequency 106 is (30 – 40). So, the corresponding values from the median class are L = 30, pcf = 77, f =  40 and c =10. 

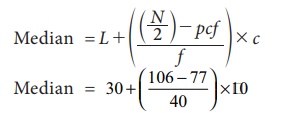
Median = 37.25 (corrected to two places of decimals)

Calculations proceeded for mean deviation about the median.

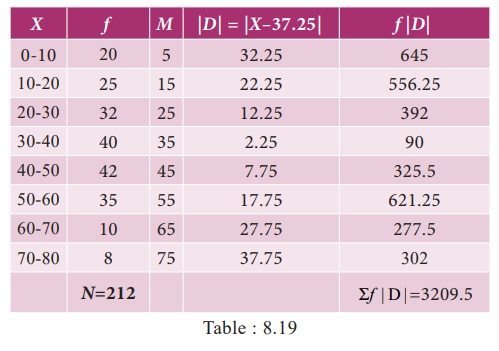
Then the mean deviation about median is to be computed by the following

NOTE

The above problem can also be solved for mean deviation about mean instead of median.

Exercise 8.1

1. Find the first quartile and third quartile for the given observations.

2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22

2. Find Q₁ , Q₃, D₈ and P₆₇ of the following data :

3. Find lower quartile, upper quartile, 7th decile, 5th decile and 60th percentile for the following frequency distribution.

4. Calculate GM for the following table gives the weight of 31 persons in sample survey.

5. The price of a commodity increased by 5% from 2004 to 2005 , 8% from 2005 to 2006 and 77% from 2006 to 2007 . Calculate the average increase from 2004 to 2007?

6. An aeroplane flies, along the four sides of a square at speeds of 100,200,300 and 400 kilometres per hour respectively. What is the average speed of the plane in its flight around the square.

7. A man travelled by car for 3 days. He covered 480 km each day. On the first day he drove for 10 hours at 48 km. an hour. On the second day, he drove for 12 hours at 40 km an hour and for the last day he drove for 15 hours at 32 km. What is his average speed?

8. The monthly incomes of 8 families in rupees in a certain locality are given below. Calculate the mean, the geometric mean and the harmonic mean and confirm that the relations among them holds true. Verify their relationships among averages.

9. Calculate AM, GM and HM and also verify their relations among them for the following data

10. Calculate AM, GM and HM from the following data and also find its relationship:

11. Calculate the quartile deviation and its coefficient from the following data:

12. Calculate quartile deviation and its relative measure from the following data:

13. Compute mean deviation about median from the following data:

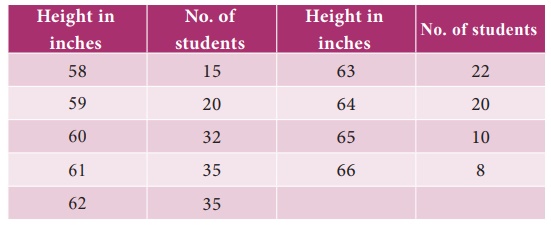
14. Compute the mean deviation about mean from the following data:

15. Find out the coefficient of mean deviation about median in the following series