Points to remember

Points to remember

• If x₁, x₂ are the x-coordinates of two points on the x-axis then the distance between them is x₂– x₁, if x₂ > x₁.

• If y₁, y₂ are the y-coordinates of two points on the y-axis then the distance between them is | y₁ – y₂ |.

• Distance between the two points ( x₁, y₁ ) and (x₂, y₂) is √{ (x_{2 −} x₁)² + (y₂ − y₁)²}

• Distance between ( x₁, y₁) and the origin (0, 0) is √{x₁² + y₁²}

• The mid-point M of the line segment joining the points A(x₁, y₁) and B(x₂, y₂ ) is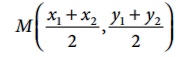 

• The point P which divides the line segment joining the two points A(x₁, y₁) and  B(x₂ , y₂ ) internally in the ratio m:n is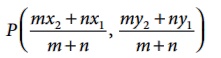 

• The centroid G of the triangle whose vertices are A (x₁ , y₁ ), B (x₂ , y₂ ) and C (x₃ , y₃ ) is

• The centroid of the triangle obtained by joining the mid-points of the sides of a triangle is the same as the centroid of the original triangle.

Activity

Plot the points A( 1, 0), B ( –7, 2), C (–3, 7) on a graph sheet and join them to form a triangle.

Plot the point G ( –3, 3).

Join AG and extend it to intersect BC at D.

Join BG and extend it to intersect AC at E.

What do you infer when you measure the distance between BD and DC and the distance between CE and EA?

Using distance formula find the lengths of CG and GF, where F in on AB.

Write your inference about AG: GD, BG: GE and CG: GF.

Note:

G is the centroid of the triangle and AD, BE and CF are the three medians of the triangle.