Numerical Problems with Answers, Solution | Coordinate Geometry | Maths - Student Activity Questions and Answers | 9th Maths : UNIT 5 : Coordinate Geometry
Chapter: 9th Maths : UNIT 5 : Coordinate Geometry
Student Activity Questions and Answers
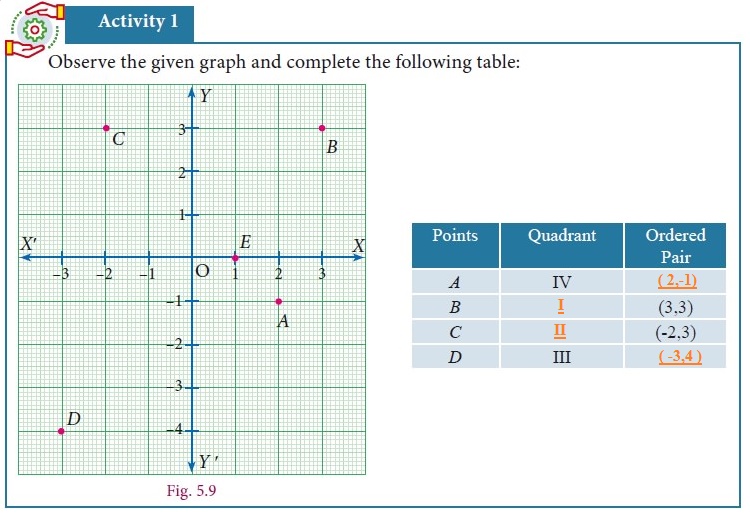

Activity – 1
Plot the following points on a graph sheet by taking the scale as 1cm = 1 unit.
Find how far the points are from each other?
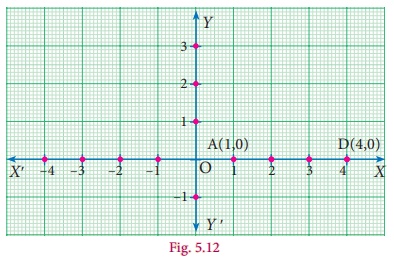
A (1, 0) and D (4, 0). Find AD and also DA.
Is AD = DA?
You plot another set of points and verify your Result.
Solution:
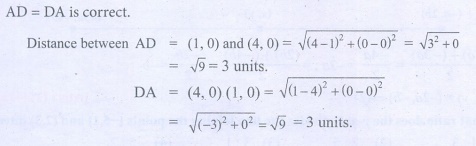

Progress Check
(i) Let X be the mid-point of the line segment joining A(3, 0) and B(−5, 4) and Y be the mid-point of the line segment joining P(−11, −8) and Q(8, −2) . Find the mid-point of the line segment XY.
(ii) If (3, x) is the mid-point of the line segment joining the points A(8, −5) and B(−2,11) , then find the value of ‘x ’.
Thinking Corner
A(6,1), B(8, 2) and C(9, 4) are three vertices of a parallelogram ABCD taken in order. Find the fourth vertex D. If (x1 , y1), (x 2 , y2 ), (x 3 , y3 ) and (x 4 , y 4 ) are the four vertices of the parallelogram, then using the given points, find the value of (x1 + x3 − x 2 , y1 + y 3 − y2 ) and state the reason for your result.
Thinking Corner
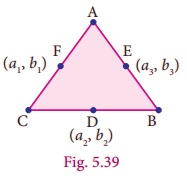
If (a1 , b1), (a2 , b2 ) and (a3 , b3 ) are the mid-points of the sides of a triangle, using the mid-points given in example 5.15 find the value of (a1 + a3 − a2 , b1 + b3 − b2 ), (a1 + a2 − a3 , b1 + b2 − b3 ) and (a2 + a3 − a1 , b2 + b3 − b1) . Compare the results. What do you observe? Give reason for your result?

Progress Check
(i) Find the coordinates of the points of trisection of the line segment joining ( 4, −1) and ( −2, −3) .
(ii) Find the coordinates of points of trisection of the line segment joining the point ( 6, −9) and the origin.
Thinking Corner
(i) What happens when m = n = 1? Can you identify it with a result already proved?
(ii) AP : PB = 1 : 2 and AQ : QB = 2:1. What is AP : AB? What is AQ : AB?
Note
• The line joining the points (x1 , y1) and (x2 , y2 ) is divided by x-axis in the ratio -y1/ y2 and by y-axis in the ratio −x1/ x1.
• If three points are collinear, then one of the points divide the line segment joining the other two points in the ratio r : 1.
• Remember that the section formula can be used only when the given three points are collinear.
• This formula is helpful to find the centroid, incenter and excenters of a triangle. It has applications in physics too; it helps to find the center of mass of systems, equilibrium points and many more.
Activity – 2
1. Draw ΔABC with vertices A(x1 , y1), B(x2, y2) and C(x3, y3) on the graph sheet.
2. Draw medians and locate the centroid of ΔABC
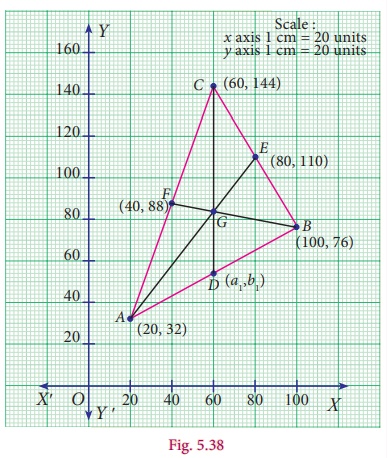
Observation
(i) The coordinates of the vertices of ABC where
A(x1 , y1) = 20,32,
B(x2 , y2 ) = 100,76
and C(x3 , y3 ) = 60,144
(ii) The coordinates of the centroid G = [x1+x2+x1]/3 , [y1+y2+y1]/3
(iii) Use the formula to locate the centroid, whose coordinates are = 60,84.
(iv) Mid-point of AB is 60,54.
(v) Find the point which divides the line segment joining (x3 , y3 ) and the mid-point of AB internally in the ratio 2:1 is 60,84.
Note
• The medians of a triangle are concurrent and the point of concurrence, the centroid G, is one-third of the distance from the opposite side to the vertex along the median.
• The centroid of the triangle obtained by joining the mid-points of the sides of a triangle is the same as the centroid of the original triangle.
Note
• The Euler line of a triangle is the line that passes through the orthocenter (H), centroid (G) and the circumcenter (S). G divides the line segment ![]() in the ratio 2:1 from the orthocenter. That is centroid divides orthocenter and circumcenter internally in the ratio 2:1 from the Orthocentre.
in the ratio 2:1 from the orthocenter. That is centroid divides orthocenter and circumcenter internally in the ratio 2:1 from the Orthocentre.
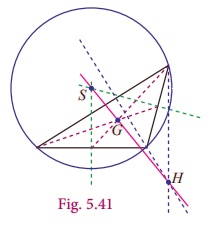
• In an equilateral triangle, orthocentre, incentre, centroid and circumcentre are all the same.
Thinking Corner
(i) Master gave a trianglular plate with vertices A(5, 8), B(2,4), C(8, 3) and a stick to a student. He wants to balance the plate on the stick. Can you help the boy to locate that point which can balance the plate.
(ii) Which is the centre of gravity for this triangle? why?
Activity
Plot the points A( 1, 0), B ( –7, 2), C (–3,
7) on a graph sheet and join them to form a triangle.
Plot the point G ( –3, 3).
Join AG and extend it to intersect BC at D.
Join BG and extend it to intersect AC at E.
What do you infer when you measure the distance between BD
and DC and the distance between CE and EA?
Using distance formula find the lengths of CG and GF,
where F in on AB.
Write your inference about AG: GD, BG: GE and CG: GF.
Note:
G is the centroid of the triangle and AD,
BE and CF are the three medians of the
triangle.
Related Topics