Points of Trisection of a Line Segment

Points of Trisection of a Line Segment

The mid-point of a line segment is the point of bisection, which means dividing into two parts of equal length. Suppose we want to divide a line segment into three parts of equal length, we have to locate points suitably to effect a trisection of the segment.

For a given line segment, there are two points of trisection. The method of obtaining this is similar to that of what we did in the case of locating the point of bisection (i.e., the mid-point). Observe the given Fig. 5.31. Here P and Q are the points of trisection of the line segment AB where A is ( x₁ , y₁ ) and B is ( x₂ , y₂ ) . Clearly we know that, P is the mid-point of AQ and Q is the mid-point of PB. Now consider the ΔACQ and ΔPDB (Also, can be verified using similarity property of triangles which will be dealt in detail in higher classes).

A′P′ = P′Q′ = Q′B′

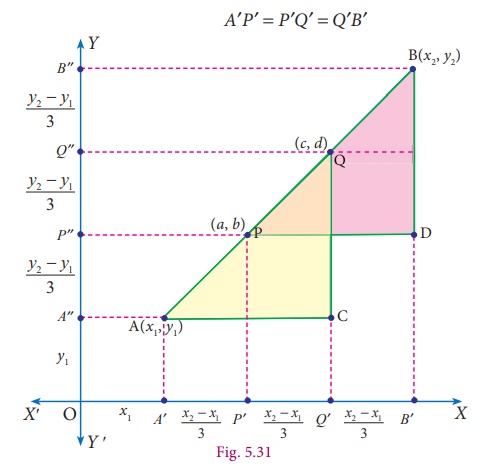
Note that when we divide the segment into 3 equal parts, we are also dividing the horizontal and vertical legs into three equal parts.

Example 5.16

Find the points of trisection of the line segment joining (−2, −1) and (4, 8) .

Solution

Let A (−2, −1) and B (4, 8) are the given points.

Let P (a,b) and Q (c, d) be the points of trisection of AB, so that AP=PQ=QB.

By the formula proved above,

P is the point

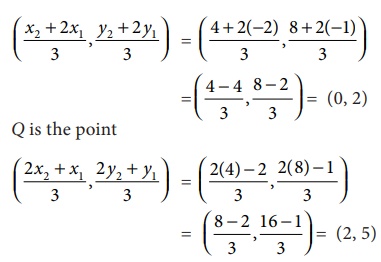
Progress Check

(i) Find the coordinates of the points of trisection of the line segment joining ( 4, −1) and ( −2, −3) .

(ii) Find the coordinates of points of trisection of the line segment joining the point ( 6, −9) and the origin.