Numerical Problems with Answers, Solution | Coordinate Geometry | Maths - Exercise 5.4: Points of Trisection of a Line Segment, Section Formula | 9th Maths : UNIT 5 : Coordinate Geometry
Chapter: 9th Maths : UNIT 5 : Coordinate Geometry
Exercise 5.4: Points of Trisection of a Line Segment, Section Formula
Coordinate Geometry
Points of Trisection of a Line Segment,
Section Formula
Exercise 5.4
1. Find the coordinates of the point which divides the line
segment joining the points A(4, −3) and B(9, 7) in
the ratio 3:2.
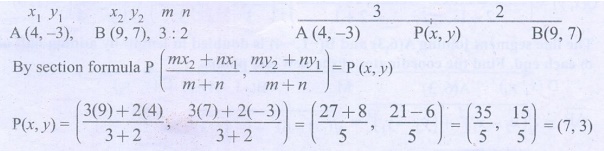
2. In what ratio does the point P(2,
−5) divide
the line segment joining A(−3, 5) and B(4, −9)
.
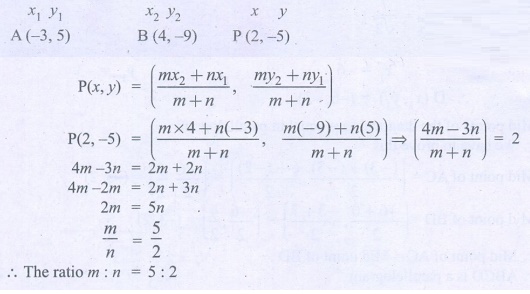
3. Find the coordinates of a point P on the line segment joining A(1, 2) and B(6, 7) in such a way that AP = 2/5 AB.
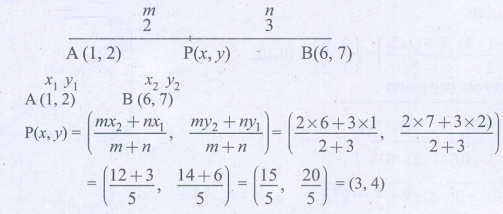
4. Find the coordinates of the points
of trisection of the line segment joining the points A(−5, 6)
and B(4, −3) .
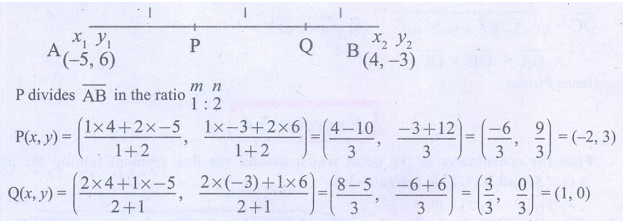
5. The line segment joining A(6,3)
and B(−1, −4) is doubled in length by adding half of AB to each end.
Find the coordinates of the new end points.

6. Using section formula, show that the
points A(7, −5), B(9, −3) and C(13,1) are collinear.

7. A line segment AB is increased
along its length by 25% by producing it to C on the side of B. If
A and B have the coordinates (−2, −3) and (2,1) respectively, then find
the coordinates of C.

Related Topics