Coordinate Geometry | Maths - Devising a Coordinate System | 9th Maths : UNIT 5 : Coordinate Geometry
Chapter: 9th Maths : UNIT 5 : Coordinate Geometry
Devising a Coordinate System
Devising a Coordinate System
You ask your friend to draw a rectangle on a blank sheet of paper, 5 cm by 3 cm. He says, “Sure, but where on this sheet ?” How would you answer him ?
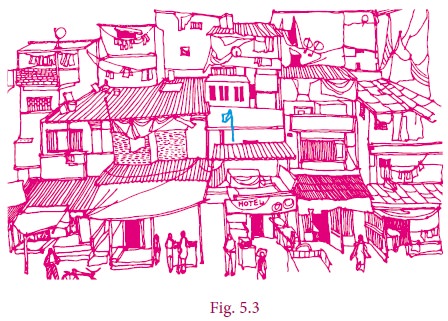
Now look at the picture. How will you describe it to another person?
Let us analyse the given picture (Fig. 5.3). Just like that a particular house is to be pointed out, it is going to be a difficult task. Instead, if any place or an object is fixed for identification then it is easy to identify any other place or object relative to it. For example, you fix the flag and talk about the house to the left of it, the hotel below it, the antenna on the house to right of it etc.
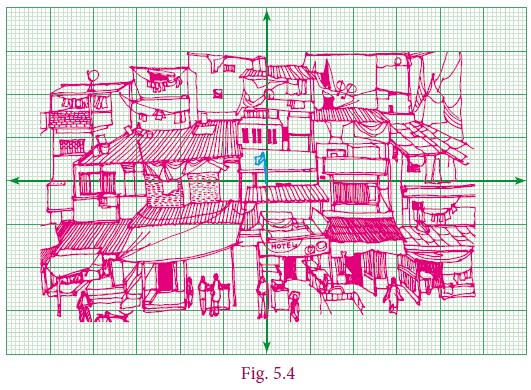
As shown Fig. 5.4 you draw two perpendicular lines in such a way that the flag is pointed out, near the intersection point. Now if you tell your friend the total length and width of the picture frame, keeping the flagpole as landmark, you can also say 2 cm to the right, 3 cm above etc. Since you know directions, you can also say 2 cm east, 3 cm north.
This is what we are going to do. A number line is usually represented as horizontal line on which the positive numbers always lie on the right side of zero, negative on the left side of zero. Now consider another copy of the number line, but drawn vertically: the positive integers are represented above zero and the negative integers are below zero (fig 5.5).
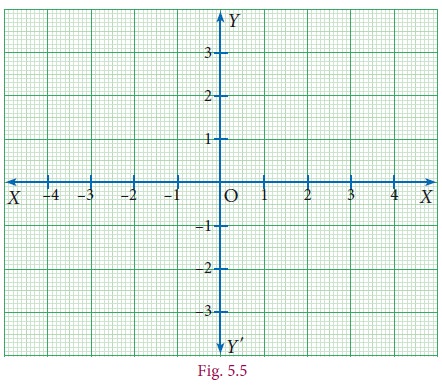
Where do the two number lines meet ? Obviously at zero for both lines. That will be our “flag”, the fixed location. We can talk of other numbers relative to it, on both the lines. But now you see that we talk not only of numbers on the two number lines but lots more !
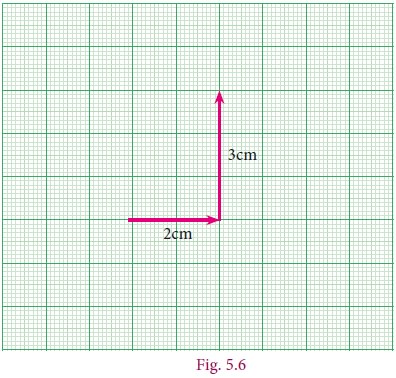
Suppose we go 2 to the right and then 3 to the top. We would call this place (→2,↑3)
All this vertical, horizontal, up, down etc is all very cumbersome. We simply say (2,3) and understand this as 2 to the right and then 3 up. Notice that we would reach the same place if we first went 3 up and then 2 right, so for us, the instruction (2,3) is not the same as the instruction (3,2). What about (–2,3) ? It would mean 2 left and 3 up. From where ? Always from 0,0). What about the instruction (2,–3)?

It would mean 2 right and 3 down. We need names for horizontal and vertical number lines too. We call the horizontal number line the x-axis and the vertical number line the y-axis. To the right we mark it as X, to the left as X’, to the top as Y, to the bottom as Y’.
The x-co-ordinate is called the abscissa and the y-co-ordinate is called the ordinate. We call the meeting point of the axes (0,0) the origin.
Now we can describe any point on a sheet of paper by a pair (x,y). However, what do (1, 2) etc mean on our paper ? We need to choose some convenient unit and represent these numbers. For instance we can choose 1 unit to be 1 cm. Thus (2,3) is the instruction to move 2 cm to the right of (0,0) and then to move 3 cm up. Please remember that the choice of units is arbitrary: if we fix 1 unit to be 2 cm, our figures will be larger, but the relative distances will remain the same.
In fact, we now have a language to describe all the infinitely many points on the plane, not just our sheet of paper !
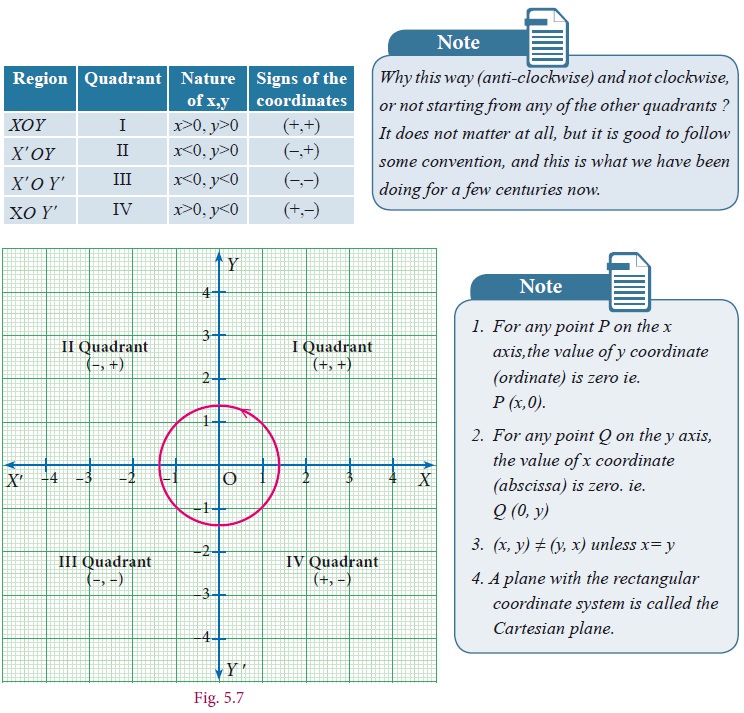
Since the x-axis and the y-axis divide the plane into four regions, we call them quadrants. (Remember, quadrilateral has 4 sides, quadrants are 4 regions.) They are usually numbered as I, II, III and IV, with I for upper east side, II for upper west side, III for lower west side and IV for lower east side, thus making an anti-clockwise tour of them all.
1. Plotting Points in Cartesian Coordinate Plane
To plot the points (4, 5) in the Cartesian coordinate plane.
We follow the x – axis until we reach 4 and draw a vertical line at x = 4.
Similarly, we follow the y – axis until we reach 5 and draw a horizontal line at y = 5.
The intersection of these two lines is the position of (4, 5) in the Cartesian plane.
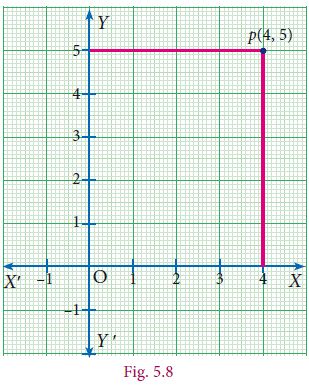
This point is at a distance of 4 units from the y-axis and 5 units from the x-axis.
Thus the position of (4, 5) is located in the Cartesian plane.
Example 5.1
In which quadrant does the following points lie?
(a) (3,–8) (b) (–1,–3) (c) (2, 5) (d) (–7, 3)
Solution
1. The x- coordinate is positive and y – coordinate is negative. So, Point(3,–8) lies in the IV quadrant.
2. The x-coordinate is negative and y – coordinate is negative. So, Point(–1,–3) lies in the quadrant.
3. The x-coordinate is positive and y – coordinate is positive. So Point(2,5) lies in the quadrant.
4. The x-coordinate is negative and y – coordinate is positive. So, Point(–7,3) lies in the II quadrant
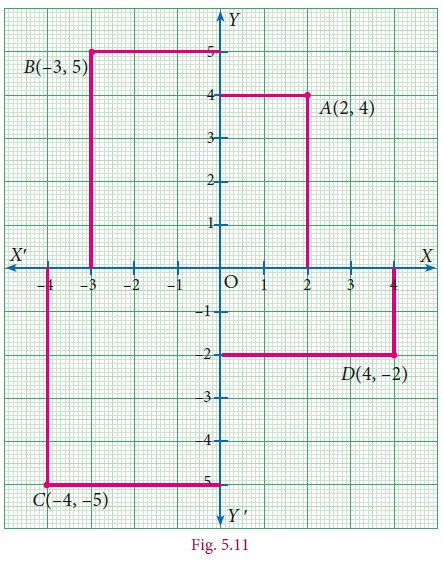
Example 5.2
Plot the points A(2,4), B(–3,5), C(–4,–5), D(4,–2) in the Cartesian plane.
Solution
1. To plot (2, 4), draw a vertical line at x = 2 and draw a horizontal line at y = 4. The intersection of these two lines is the position of (2, 4) in the Cartesian plane. Thus, the Point A (2, 4) is located in the I quadrant of Cartesian plane.
2. To plot (–3, 5), draw a vertical line at x = –3 and draw a horizontal line at y = 5. The intersection of these two lines is the position of (–3, 5) in the Cartesian plane. Thus, the Point B (–3, 5) is located in the II quadrant of Cartesian plane.
3. To plot (–4, –5), draw a vertical line at x =–4 and draw a horizontal line at y = –5. The intersection of these two lines is the position of (-4, 5) in the Cartesian plane. Thus, the Point C (–4, –5) is located in the III quadrant of Cartesian plane.
4. To plot (4, –2), draw a vertical line at x = 4 and draw a horizontal line at y = –2. The Intersection of these two lines is the position of (4,–2) in the Cartesian plane. Thus, the Point D (4,–2) is located in the IV quadrant of Cartesian plane.
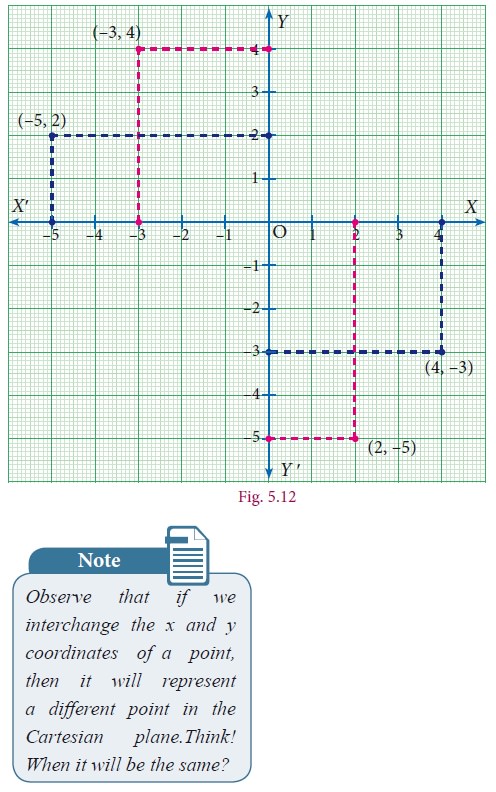
Example 5.3
Locate the points
(i) (2,–5) and (–5, 2) (ii) (–3, 4) and (4,–3) in the rectangular coordinate system.
Solution
Example 5.4
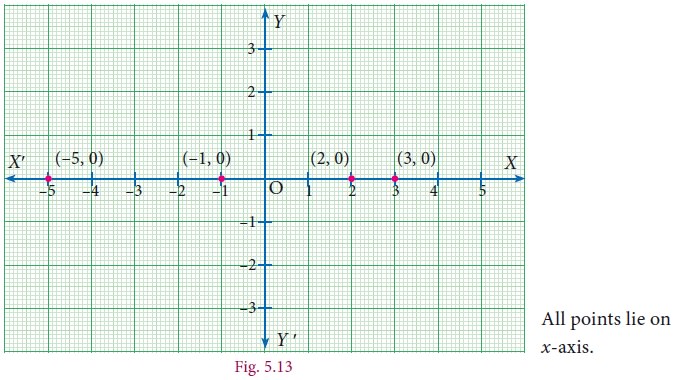
Plot the following points (2, 0), (–5, 0), (3, 0), (–1, 0) in the Cartesian plane. Where do they lie?
Solution
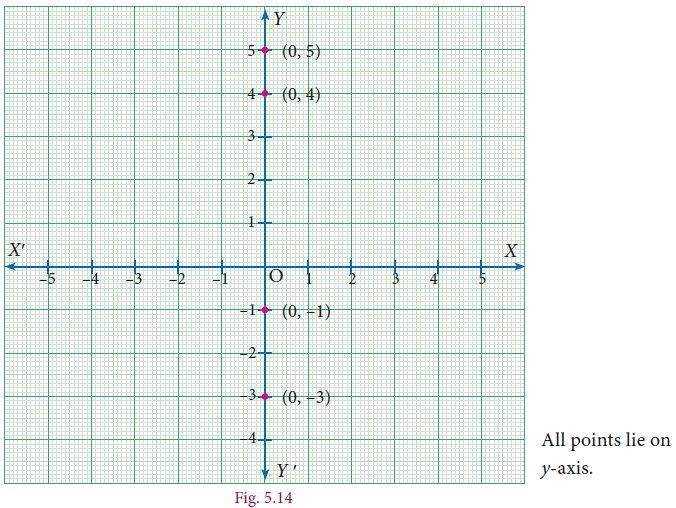
Example 5.5
Plot the following points (0,–3),(0,4),(0,–1),(0,5) in the Cartesian plane. Where do they lie?
Solution
Example 5.6
Plot the points (–4,3),(–3,3),(–1,3),(0,3),(3,3) in the Cartesian Plane. What can you say about the position of these points?
Solution
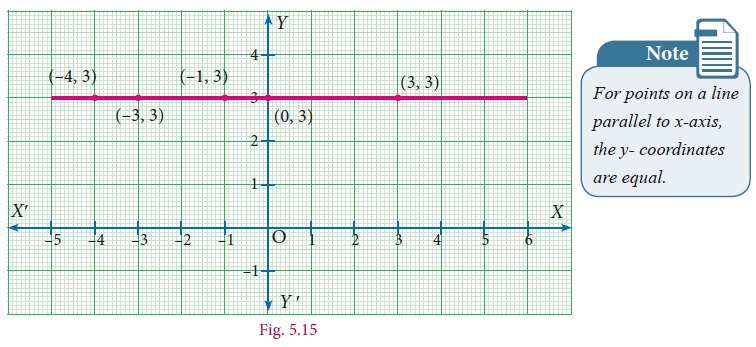
When you join these points, you see that they lie on a line which is parallel to x-axis.
Example 5.7
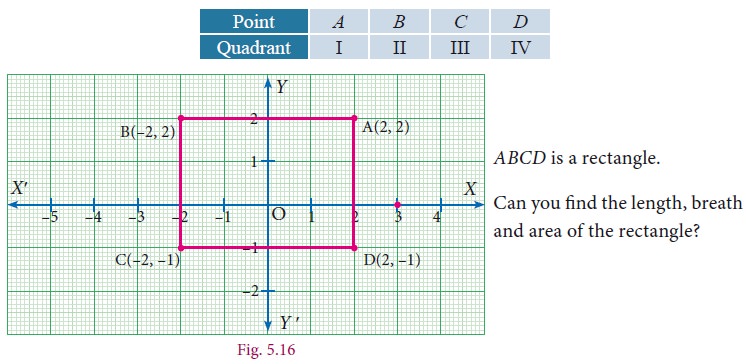
Plot the following points A(2,2), B(–2,2), C(–2,–1), D(2,–1) in the Cartesian plane . Discuss the type of the diagram by joining all the points taken in order.
Solution
Related Topics