Exercise 5.6: Multiple Choice Questions

Coordinate Geometry

Exercise 5.6

Multiple Choice Questions

1. If the y-coordinate of a point is zero, then the point always lies ______

(1) in the I quadrant

(2) in the II quadrant

(3) on x-axis

(4) on y-axis

Solution:

Points in x - axis has y - coordinate zero

[Answer: (3) on x-axis]

2. The points (–5, 2) and (2, –5) lie in the ________

(1) same quadrant

(2) II and III quadrant respectively

(3) II and IV quadrant respectively

(4) IV and II quadrant respectively

Solution:

 (–, +) lies II^nd quadrant and (+,–) lies in IV^th quadrant

[Answer: (3) II and IV quadrant respectively]

3. On plotting the points O(0,0), A(3, – 4), B(3, 4) and C(0, 4) and joining OA, AB, BC and CO, which of the following figure is obtained?

(1) Square

(2) Rectangle

(3) Trapezium

(4) Rhombus

Solution:

In trapezium one pair of opposite side is parallel.

[Answer: (3) Trapezium]

4. If P( –1,1), Q( 3,–4), R( 1, –1), S(–2, –3) and T( –4, 4) are plotted on a graph paper, then the points in the fourth quadrant are __________

(1) P and T

(2) Q and R

(3) only S

(4) P and Q

Solution:

Points in IV^th quadrant are (+,–)

[Answer: (2) Q and R]

5. The point whose ordinate is 4 and which lies on the y-axis is _______________

(1)( 4, 0 )

(2) (0, 4)

(3) (1, 4)

(4) (4, 2)

Solution:

Points in y-axis have abscissa a zero

[Answer: (2) (0, 4)]

6. The distance between the two points ( 2, 3 ) and ( 1, 4 ) is ______

(1) 2

(2) √56

(3)  √10

(4) √2

Solution:

Distance = √[(x₂–x₁)²+(y₂–y₁)²]

[Answer: (4) √2]

7. If the points A (2,0), B (-6,0), C (3, a–3) lie on the x-axis then the value of a is _____

(1) 0

(2) 2

(3) 3

(4) –6

Solution:

Points in y-axis have ordinate zero.

a–3 = 0

⇒ a = 3

[Answer: (3) 3]

8. If ( x+2, 4) = (5, y–2), then the coordinates (x,y) are _____

(1) (7, 12)

(2) (6, 3)

(3) (3, 6)

(4) (2, 1)

Solution:

 x + 2 = 5 ⇒ x = 3; y – 2 = 4 ⇒ y = 6

[Answer: (3) (3, 6)]

9. If Q₁, Q₂, Q₃, Q₄ are the quadrants in a Cartesian plane then Q₂ ∩ Q₃ is ___________

 (1) Q₁∩ Q₂

(2) Q₂∩Q₃

(3) Null set

(4) Negative x-axis.

Solution:

Quadrants do not contain the axis.

[Answer: (3) Null set]

10. The distance between the point ( 5, –1 ) and the origin is _________

(1) √24

(2) √37

(3) √26

(4) √17

Solution:

Distance = √[(5-0)² + (–1 – 0)²] = √[5²+l²] = √26

[Answer: (3) √26]

11. The coordinates of the point C dividing the line segment joining the points P(2,4) and Q(5,7) internally in the ratio 2:1 is

(1) (7/2, 11/2)

(2) (3,5)

(3) (4,4)

(4) (4,6)

Solution:

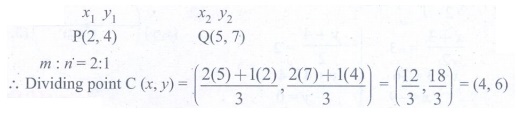
[Answer: (4) (4,6)]

12. If P (a/3,b/2) is the mid-point of the line segment joining A(−4,3) and B(−2,4) then (a,b) is

(1) (−9,7)

(2) (−3, 7/2)

(3) (9, −7)

(4) ( 3, −7/2 )

Solution:

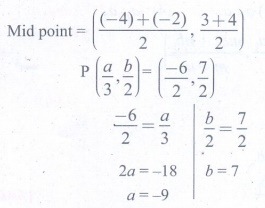
[Answer: (1) (−9,7)]

13. In what ratio does the point Q(1,6) divide the line segment joining the points P(2,7) and R(−2,3)

(1) 1:2

(2) 2:1

(3) 1:3

(4) 3:1

Solution:

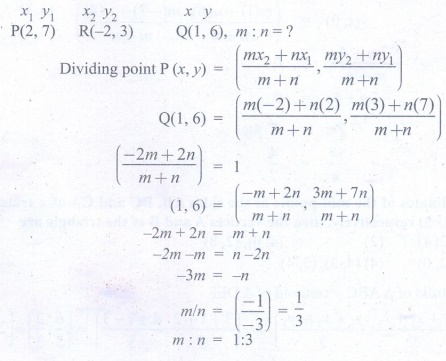
[Answer: (3) 1:3]

14. If the coordinates of one end of a diameter of a circle is (3,4) and the coordinates of its centre is (−3,2), then the coordinate of the other end of the diameter is

(1) (0,−3)

(2) (0,9)

(3) (3,0)

(4) (−9,0)

Solution:

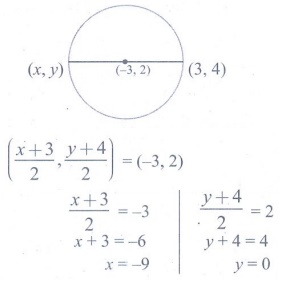
[Answer: (4) (−9,0)]

15. The ratio in which the x-axis divides the line segment joining the points A(a₁ ,b₁ ) and B (a₂ ,b₂ ) is

(1) b₁ : b₂

(2) −b₁ : b₂

(3) a₁ : a₂

(4) −a₁ : a₂

Solution:

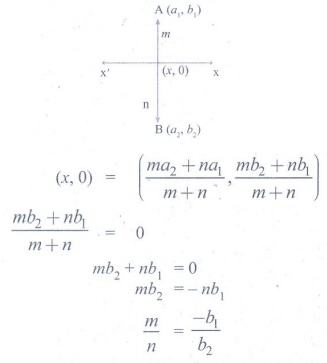
[Answer: (2) −b₁ : b₂]

16. The ratio in which the x-axis divides the line segment joining the points (6,4) and (1, −7) is

(1) 2:3

(2) 3:4

(3) 4:7

(4) 4:3

Solution:

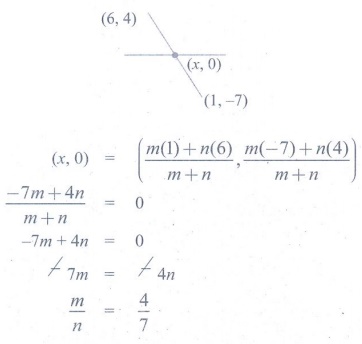
[Answer: (3) 4:7]

17. If the coordinates of the mid-points of the sides AB, BC and CA of a triangle are (3,4), (1,1) and (2,−3) respectively, then the vertices A and B of the triangle are

(1) (3,2), (2,4)

(2) (4,0), (2,8)

(3) (3,4), (2,0)

(4) (4,3), (2,4)

Solution:

[Answer: (2) (4,0), (2,8)]

18. The mid-point of the line joining (−a,2b) and (−3a,−4b) is

(1) (2a,3b)

(2) (−2a, −b)

(3) (2a,b)

(4) (−2a, −3b)

Solution:

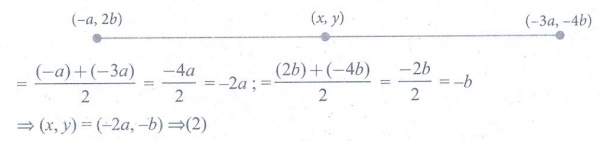
[Answer: (2) (−2a, −b)]

19. In what ratio does the y-axis divides the line joining the points (−5,1) and (2,3) internally

(1) 1:3

(2) 2:5

(3) 3:1

(4) 5:2

Solution:

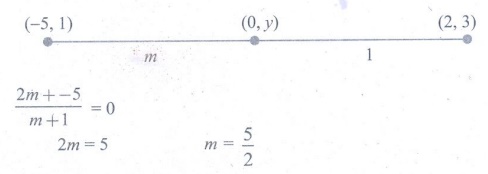
[Answer: (4) 5:2]

20. If (1,−2), (3,6), (x,10) and (3,2) are the vertices of the parallelogram taken in order, then the value of x is

(1) 6

(2) 5

(3) 4

(4) 3

Solution:

In parallelogram diagonals bisect each other.

Mid point of AC = Mid point of BD

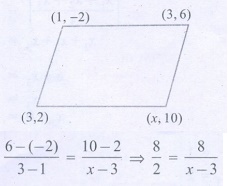
6− (−2) / 3−1 = 10−2 / x−3

8/2 = 8/x−3

x−3 = 2

 x = 5

[Answer: (2) 5]