The Coordinates of the Centroid

The Coordinates of the Centroid

Consider a ΔABC whose vertices are A( x₁ , y₁), B ( x₂ , y₂ ) and C ( x₃ , y₃ ).

Let AD, BE and CF be the medians of the ΔABC.

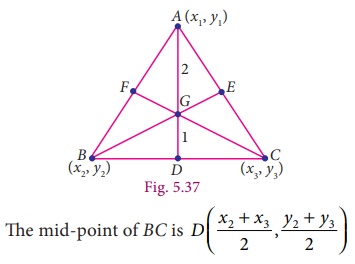
The centroid G divides the median AD internally in the ratio 2:1 and therefore by section formula, the centroid

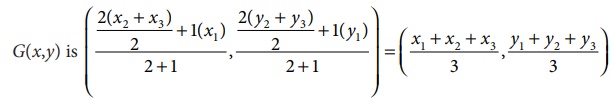
The centroid G of the triangle with vertices A(x₁ , y₁), B (x ₂ , y₂ ) and C (x ₃ , y₃ ) is

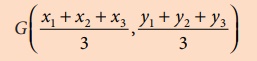
Activity – 2

1. Draw ΔABC with vertices A(x₁ , y₁), B(x₂, y₂) and C(x₃, y₃) on the graph sheet.

2. Draw medians and locate the centroid of ΔABC

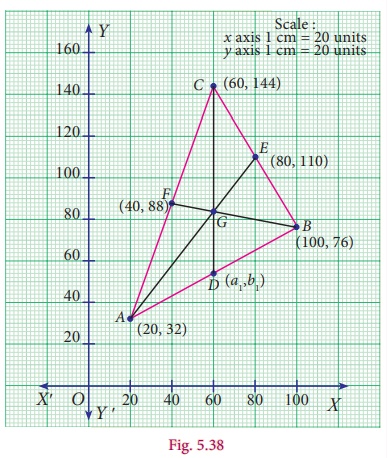
Observation

(i) The coordinates of the vertices of ABC where

A(x₁ , y₁) = 20,32,

 B(x₂ , y₂ ) = 100,76

 and C(x₃ , y₃ ) = 60,144

(ii) The coordinates of the centroid G = [x1+x2+x1]/3 , [y1+y2+y1]/3

(iii) Use the formula to locate the centroid, whose coordinates are = 60,84.

(iv) Mid-point of AB is 60,54.

(v) Find the point which divides the line segment joining (x₃ , y₃ ) and the mid-point of AB internally in the ratio 2:1 is 60,84.

Note

• The medians of a triangle are concurrent and the point of concurrence, the centroid G, is one-third of the distance from the opposite side to the vertex along the median.

• The centroid of the triangle obtained by joining the mid-points of the sides of a triangle is the same as the centroid of the original triangle.

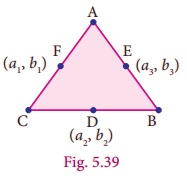
• If (a₁, b₁), (a₂, b₂) and (a₃, b₃) are the mid-points of the sides of a triangle ABC then its centroid G is given by

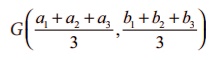
Example 5.20

Find the centroid of the triangle whose veritices are A(6, −1), B(8, 3) and C(10, −5).

Solution

The centroid G(x, y) of a triangle whose vertices are (x₁ , y₁), (x₂ , y₂ ) and (x₃ , y₃ ) is given by

We have (x₁ , y₁ ) = (6, −1); (x₂ , y₂ ) = (8, 3);

(x₃ , y₃ ) = (10, −5)

The centroid of the triangle

Note

• The Euler line of a triangle is the line that passes through the orthocenter (H), centroid (G) and the circumcenter (S). G divides the line segment  in the ratio 2:1 from the orthocenter. That is centroid divides orthocenter and circumcenter internally in the ratio 2:1 from the Orthocentre.

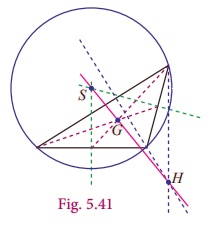
• In an equilateral triangle, orthocentre, incentre, centroid and circumcentre are all the same.

Example 5.21

If the centroid of a triangle is at ( −2,1) and two of its vertices are (1, −6) and ( −5, 2) , then find the third vertex of the triangle.

Solution 

Let the vertices of a triangle be

A(1, −6), B(−5, 2) and C ( x₃ , y₃ )

Given the centroid of a triangle as ( −2,1) we get,

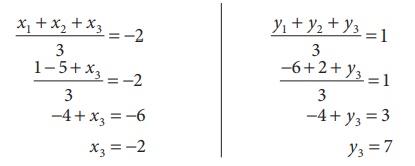
Therefore, third vertex is (−2,7).

Thinking Corner

(i) Master gave a trianglular plate with vertices A(5, 8), B(2,4), C(8, 3) and a stick to a student. He wants to balance the plate on the stick. Can you help the boy to locate that point which can balance the plate.

(ii) Which is the centre of gravity for this triangle? why?