Exercise 5.3: The Mid-point of a Line Segment

Coordinate Geometry:

The Mid-point of a Line Segment

Exercise 5.3

1. Find the mid-points of the line segment joining the points

(i) (−2,3) and (−6,−5) (ii) (8,−2) and (−8,0) (iii) (a,b) and (a+2b,2a−b) (iv) (1/2, − 3/7) and (3/2, −11/7)

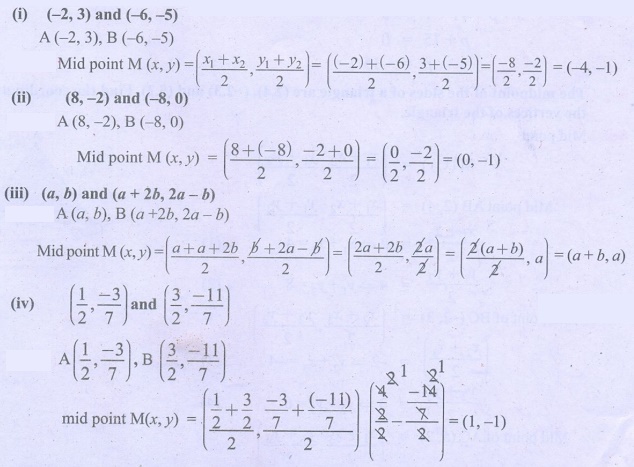
2. The centre of a circle is (−4,2). If one end of the diameter of the circle is (−3,7), then find the other end.

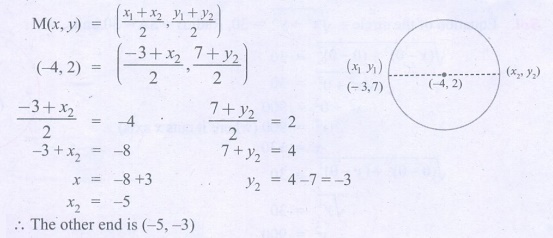
3. If the mid-point (x,y) of the line joining (3,4) and (p,7) lies on 2x + 2 y + 1 = 0 , then what will be the value of p?

4. The mid-point of the sides of a triangle are (2,4), (−2,3) and (5,2). Find the coordinates of the vertices of the triangle.

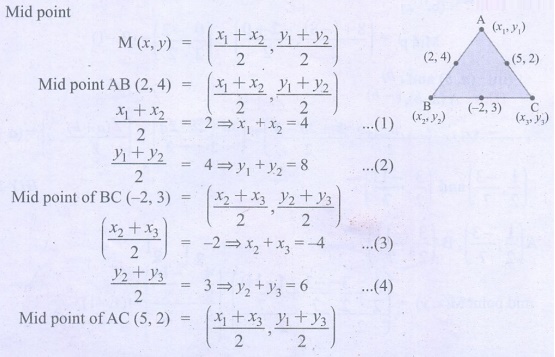
5. O(0,0) is the centre of a circle whose one chord is AB, where the points A and B are (8,6) and (10,0) respectively. OD is the perpendicular from the centre to the chord AB. Find the coordinates of the mid-point of OD.

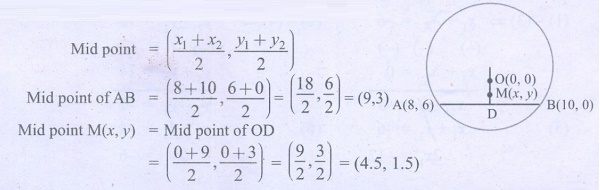
6. The points A(−5, 4) , B(−1, −2) and C(5, 2) are the vertices of an isosceles right-angled triangle where the right angle is at B. Find the coordinates of D so that ABCD is a square.

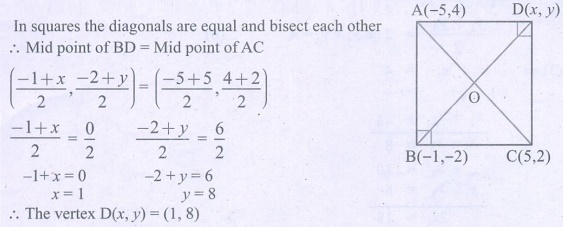
7. The points A(−3, 6) , B(0, 7) and C(1, 9) are the mid-points of the sides DE, EF and FD of a triangle DEF. Show that the quadrilateral ABCD is a parallellogram.

8. A(−3, 2) , B(3, 2) and C(−3, −2) are the vertices of the right triangle, right angled at A. Show that the mid-point of the hypotenuse is equidistant from the vertices.