Section Formula

Section Formula

We studied bisection and trisection of a given line segment. These are only particular cases of the general problem of dividing a line segment joining two points ( x_1, y₁ ) and ( x ₂ , y₂ ) in the ratio m : n.

Given a segment AB and a positive real number r.

We wish to find the coordinate of point P which divides AB in the ratio r :1.

This means AP/PB = r/1 or AP = r(PB).

This means that x – x₁ = r(x₂ – x)

Solving this, x = ( rx₂ + x₁) / (r + 1)      ….. (1)

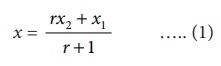
We can use this result for points on a line to the general case as follows.

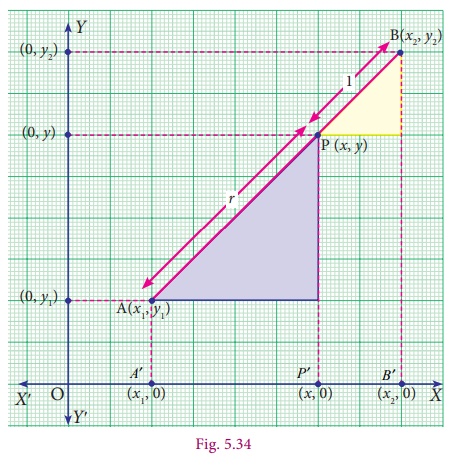
Taking AP : PB = r :1 , we get A′ P′ : P′B′ = r :1 .

Therefore A′P′ = r(P′B′)

Thus, (x − x₁ ) = r( x₂ − x)

which gives x = ( rx₂ + x₁ ) / (r + 1)   … [see (1)]

Precisely in the same way we can have y = ry₂ + y₁ / r + 1

If P is between A and B, and AP/PB = r , then we have the formula,

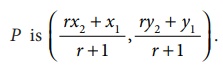
If r is taken as m/n , then the section formula is 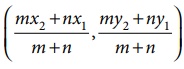 , which is the  standard form.

Thinking Corner

(i) What happens when m = n = 1? Can you identify it with a result already proved?

(ii) AP : PB = 1 : 2 and AQ : QB = 2:1. What is AP : AB? What is AQ : AB?

Note

• The line joining the points (x₁ , y₁) and (x₂ , y₂ ) is divided by x-axis in the ratio -y₁/ y₂ and by y-axis in the ratio −x₁/ x₁.

• If three points are collinear, then one of the points divide the line segment joining the other two points in the ratio r : 1.

• Remember that the section formula can be used only when the given three points are collinear.

• This formula is helpful to find the centroid, incenter and excenters of a triangle. It has applications in physics too; it helps to find the center of mass of systems, equilibrium points and many more.

Example 5.17

Find the coordinates of the point which divides the line segment joining the points (3,5) and (8,−10) internally in the ratio 3:2.

Solution

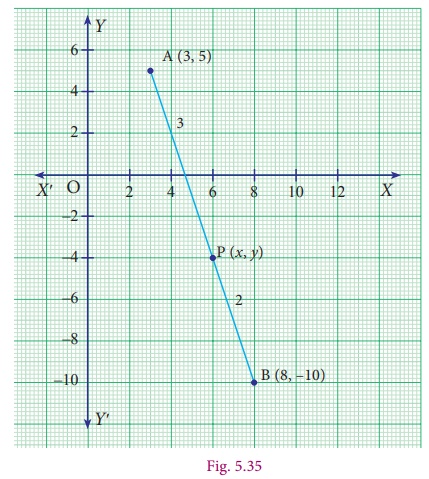
Let A(3,5), B(8,−10) be the given points and let the point P(x,y) divides the line segment AB internally in the ratio 3:2.

By section formula, P ( x, y ) =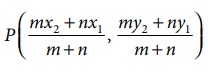 

Here x₁ = 3, y₁ = 5, x₂ = 8, y₂ = −10 and m = 3, n = 2

Therefore P ( x, y ) = 

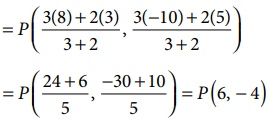
= P ( [3(8) + 2(3)] / [3+2], [3(−10) + 2(5)] / [3+2] )

= P ( [24 + 6]/5 , [−30 + 10]/5) = P(6, − 4 )

Example 5.17

In what ratio does the point P(–2, 4) divide the line segment joining the points A(–3, 6) and B(1, –2) internally?

Solution

Given points are A(–3, 6) and B(1, –2). P(–2, 4) divide AB internally in the ratio m : n.

By section formula,

m : n = 1 : 3

Hence P divides AB internally in the ratio 1:3.

Note

We may arrive at the same result by also equating the y-coordinates. Try it.

Example 5.19

What are the coordinates of B if point P(−2,3) divides the line segment joining A(−3,5) and B internally in the ratio 1:6?

Solution

Let A(−3,5) and B(x₂ , y₂ ) be the given two points.

Given P(−2,3) divides AB internally in the ratio 1:6.

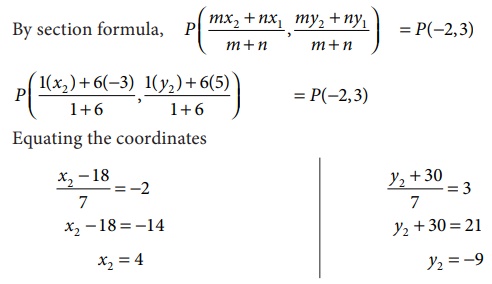
Therefore, the coordinate of B is (4, −9)