Trigonometry

TRIGONOMETRY

There is perhaps nothing which so occupies the middle position of mathematics as Trigonometry.- J. F. Herbart

Euler, like Newton, was the greatest mathematician of his generation. He studied all areas of mathematics and continued to work hard after he had gone blind. Euler made discoveries in many areas of mathematics, especially Calculus and Trigonometry. He was the first to prove  several theorems in Geometry.

Leonhard Euler (AD.(CE))170476- –1783)550)

Learning Outcomes

• To understand the relationship among various trigonometric ratios.

• To recognize the values of trigonometric ratios and their reciprocals.

• To use the concept of complementary angles.

• To understand the usage of trigonometric tables.

Introduction

Trigonometry (which comes from Greek words trigonon means triangle and metron means measure) is the branch of mathematics that studies the relationships involving lengths of sides and measures of angles of triangles. It is a useful tool for engineers, scientists, and surveyors and is applied even in seismology and navigation.

Observe the three given right angled triangles; in particular scrutinize their measures. The corresponding angles shown in the three triangles are of the same size. Draw your attention to the lengths of “opposite” sides (meaning the side opposite to the given angle) and the “adjacent” sides (which is the side adjacent to the given angle) of the triangle.

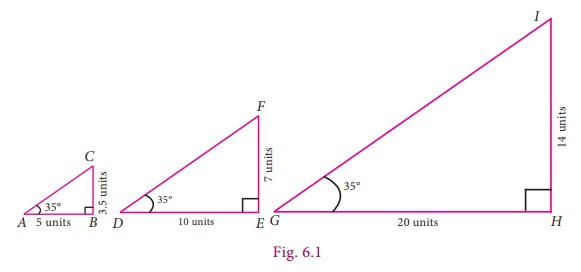
What can you say about the ratio (opposite side / adjacent side) in each case? Every right angled triangle given here has the same ratio 0.7 ; based on this finding, now what could be the length of the side marked ‘x’ in the Fig 6.2? Is it 15?

Such remarkable ratios stunned early mathematicians and paved the way for the subject of trigonometry.

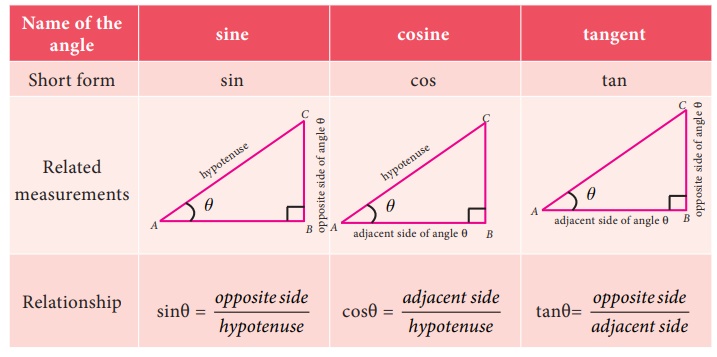
There are three basic ratios in trigonometry, each of which is one side of a right-angled triangle divided by another.

The three ratios are:

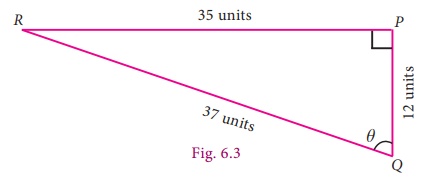
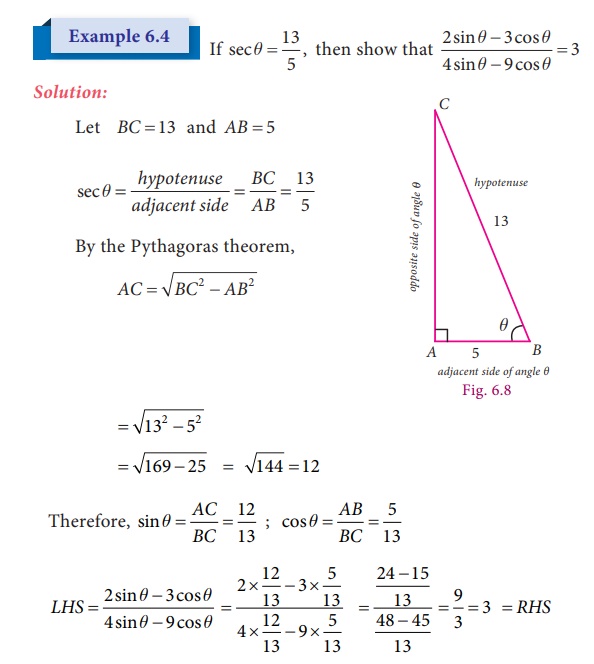
Example 6.1

For the measures in the figure, compute sine, cosine and tangent ratios of the angle θ.

Solution

In the given right angled  triangle, note that for the given angle θ, PR is the ‘opposite’ side and PQ is the ‘adjacent’ side.

It is enough to leave the ratios as fractions. In case, if you want to simplify each ratio neatly in a terminating decimal form, you may opt for it, but that is not obligatory.

Note

• Since trigonometric ratios are defined in terms of ratios of sides, they are unitless numbers.

• Ratios like sinθ, cosθ, tanθ are not to be treated like (sin)×(θ), (cos)×(θ),(tan)×(θ).

Thinking Corner

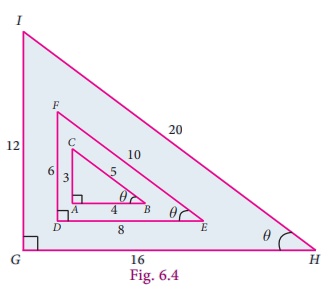
The given triangles ABC,DEF and GHI have measures 3-4-5, 6-8-10 and 12-16-20.

Are they all right triangles?

How do you know?

The angles at the vertices B, E and H are of equal size (each angle is equal to θ).

With these available details, fill up the following table and comment on the ratios that you get.

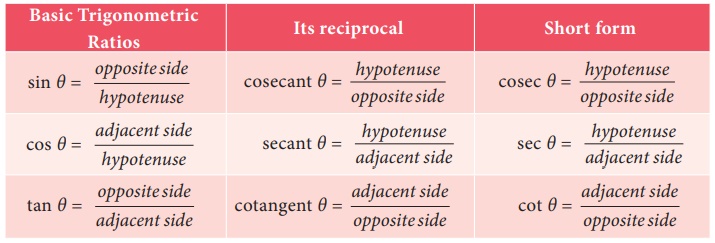
Reciprocal ratios

We defined three basic trigonometric ratios namely, sine, cosine and tangent. The reciprocals of these ratios are also often useful during calculations. We define them as follows:

From the above ratios we can observe easily the following relations:

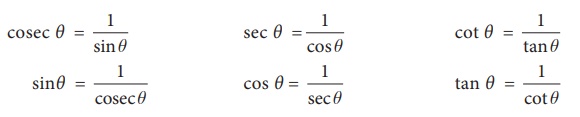
(sin θ ) × (cosec θ) = 1 . We usually write this as sin θ cosec θ 1.

(cos θ) × (sec θ) =1 . We usually write this as cos θ sec θ = 1.

(tan θ) × (cot θ) = 1. We usually write this as tan θ cot θ = 1.

Example 6.2

Find the six trigonometric ratios of the angle θ using the given diagram.

Solution

By Pythagoras theorem,

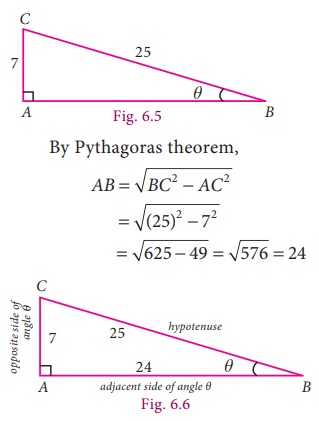
The six trignometric ratios are

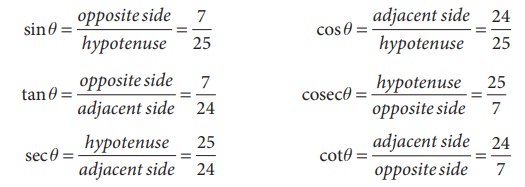
Example 6.3

If tan A = 2/3, then find all the other trigonometric ratios.

Solution

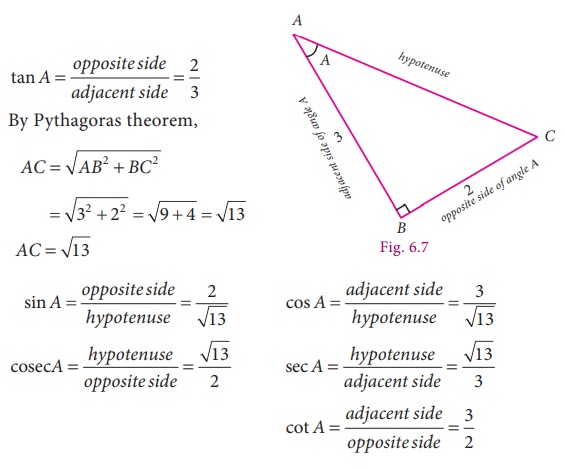
Note: We can also take the angle ‘ θ ’ at the vertex ‘C’ and proceed in the same way.