Trigonometric Ratios of Some Special Angles

Trigonometric Ratios of Some Special Angles

The values of trigonometric ratios of certain angles can be obtained geometrically.

Two special triangles come to help here.

1. Trigonometric ratios of 45°

Consider a triangle ABC with angles 45° , 45° and 90° as shown in the figure 6.9.

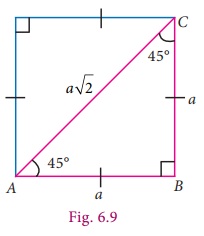
It is the shape of half a square, cut along the square’s diagonal. Note that it is also an isosceles triangle (both legs have the same length, a units).

Use Pythagoras theorem to check if the diagonal is of length a√2 .

Now, from the right-angled triangle ABC,

The reciprocals of these ratio can be easily foundout to be

cosec 45º = √2 ;

sec 45 º = √2 and

cot 45º = √1

2. Trigonometric Ratios of 30° and 60°

Consider an equilateral triangle PQR of side length 2 units.

Draw a bisector of ∠P. Let it meet QR at M.

PQ = QR = RP = 2 units.

QM = MR = 1 unit (Why?)

Knowing PQ and QM, we can find PM, using Pythagoras

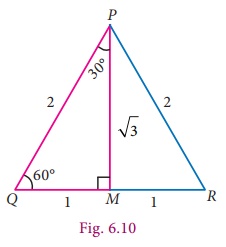
we find that PM = √3 units.

Now, from the right-angled triangle PQM,

We will use the same triangle but the other angle of measure 60° now.

3. Trigonometric ratios of 0° and 90°

To find the trigonometric ratios of 0° and 90° , we take the help of what is known as a unit circle.

A unit circle is a circle of unit radius (that is of radius 1 unit), centred at the origin.

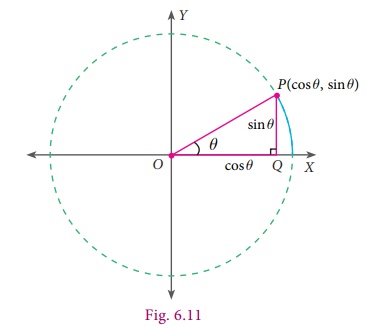
Why make a circle where the radius is 1unit?

This means that every reference triangle that we create here has a hypotenuse of 1unit, which makes it so much easier to compare angles and ratios.

We will be interested only in the positive values since we consider ‘lengths’ and it is hence enough to concentrate on the first quadrant.

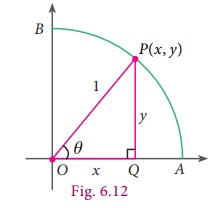
We can see that if P(x,y) be any point on the unit circle in the first quadrant and ∠POQ=θ.

 sin θ = PQ/OP = y/1 = y ; cos θ = OQ/OP = x/1 = x ; tan θ = PQ/OQ = y/x

When θ = 0º, OP coincides with OA, where A is (1,0) giving x = 1, y = 0 .

 We get thereby,

 sin 0º = 0 ; cosec 0º = not defined (why?)

 cos 0º = 1 ; sec 0º = 1

 tan 0º = 0/1 = 0 ; cot 0º = not defined (why?)

When θ = 90º, OP coincides with OB, where B is (0,1) giving x = 0, y = 1 .

 Hence,

 sin 90º = 1 ; cosec90º = 1

 cos 90º = 0 ; sec90º = not defined

 tan90º = 1/0 = not defined ; cot 90º = 0

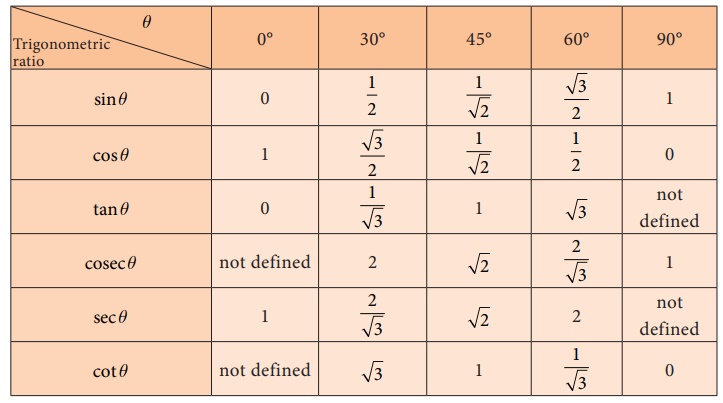
Let us summarise all the results in the table given below:

Example 6.5

Evaluate:

(i) sin 30º + cos 30º

(ii) tan 60˚ cot 60˚

(iii) [tan 45º] /  [ tan 30º + tan 60º ]

 (iv) sin²45º + cos²45º

Solution

Thinking Corner

The set of three numbers are called as Pythagorean triplets as they form the sides of a right angled triangle. For example,

(i) 3, 4, 5 (ii) 5, 12, 13 (iii) 7, 24, 25

Multiply each number in any of the above Pythagorean triplet by a non-zero constant. Verify whether each of the resultant set so obtained is also a Pythagorean triplet or not.

Example 6.6

Find the values of the following:

(i) (cos 0º + sin 45º + sin 30º)(sin 90º − cos 45º + cos 60º)

(ii) tan² 60º − 2 tan² 45º − cot² 30º + 2sin² 30º +  3/4 cosec² 45º

Solution

(i) (cos 0º + sin 45º + sin 30º)(sin 90º − cos 45º + cos 60º)

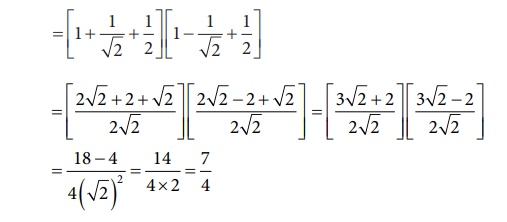
(ii) tan² 60º − 2 tan² 45º − cot² 30º + 2sin² 30º +  3/4 cosec² 45º

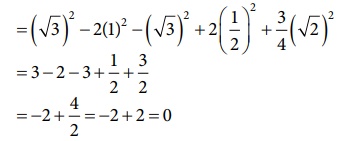
Note

(i) In a right angled triangle, if the angles are in the ratio 45° : 45° : 90° , then the sides are in the ratio 1 : 1 : √2.

(ii) Similarly, if the angles are in the ratio 30° : 60° : 90° , then the sides are in the ratio 1 : √3 : 2 .

(The two set squares in your geometry box is one of the best example for the above two types of triangles).