Trigonometric Ratios for Complementary Angles

Trigonometric Ratios for Complementary Angles

Recall that two acute angles are said to be complementary if the sum of their measures is equal to 90°.

What can we say about the acute angles of a right-angled triangle?

In a right angled triangle the sum of the two acute angles is equal to 90°. So, the two acute angles of a right angled triangle are always complementary to each other.

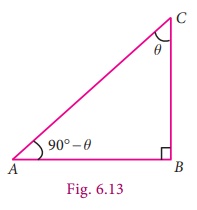
In the above figure 6.13, the triangle is right-angled at B. Therefore, if ∠C is θ , then ∠A = 90° − θ .

Example 6.7

Express (i) sin74° in terms of cosine (ii) tan12° in terms of cotangent (iii) cosec39° in terms of secant

Solution

(i) sin74° = sin(90º − 16º)       (since, 90º − 16º = 74º )

RHS is of the form sin(90º − θ) = cos θ

Therefore sin74° = cos16º

(ii) tan12° = tan(90º − 78º)       (since, 12º = 90º − 78º)

RHS is of the form tan(90º − θ) = cot θ

Therefore tan12° = cot 78º

(iii) cosec39° = cosec(90º − 51º )           (since 39º = 90º − 51° )

RHS is of the form cosec(90º − θ) sec θ

Therefore cosec39° = sec51°

Example 6.8

Evaluate: (i) sin 49° / cos 41°  (ii) sec63° / cosec 27°

Solution

(i) sin 49° / cos 41°

sin 49° = sin(90° − 41° ) = cos 41° , since 49° + 41° = 90° (complementary),

Hence on substituting sin49° = cos 41°

we get, cos41°/cos41° = 1

(ii) sec63° / cosec 27°

sec 63° sec(90° − 27° ) = cosec 27°, here 63° and 27° are complementary angles.

we have sec63° / cosec 27° = cosec 27° / cosec 27° = 1

Example 6.9

Find the values of (i) tan 7° tan 23° tan 60° tan 67° tan 83°

(ii)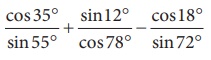 

Solution

(i) tan 7° tan 23° tan 60° tan 67° tan 83°

= tan 7° tan 83° tan 23° tan 67° tan 60° (Grouping complementary angles)

= tan 7° tan(90°-7° )tan 23° tan(90° − 23°)tan 60°

= (tan 7° . cot 7° )(tan 23° . cot 23° )tan 60°

= (1) × (1) × tan 60°

= tan60° = √3

(ii) 

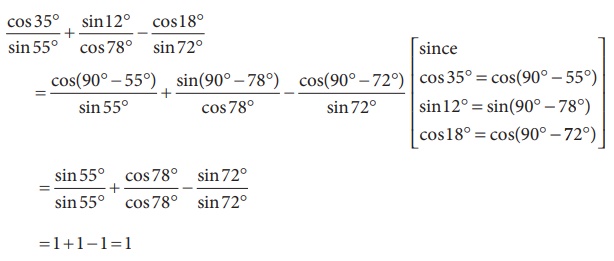
= 1 + 1 – 1 = 1

Example 6.10

(i) If cosec A = sec 34°, then find A (ii) If tan B = cot 47°, then find B.

Solution

(i) We know that cosec A = sec(90° − A)

sec(90º − A) = sec(34º)

90º - A = 34º

We get A= 90° − 34°

A = 56º

(ii) We know that tan B cot(90º - B)

cot(90º - B) = cot 47º

90º - B = 47º

We get B = 90° − 47°

B = 43º