Method of using Trigonometric Table

Method of using Trigonometric Table

We have learnt to calculate the trigonometric ratios for angles 0°, 30°, 45°, 60° and 90°. But during certain situations we need to calculate the trigonometric ratios of all the other acute angles. Hence we need to know the method of using trigonometric tables.

One degree (1°) is divided into 60 minutes (60′) and one minute (1′) is divided into 60 seconds ( 60′′ ) . Thus, 1° = 60′ and 1′ = 60′′.

The trigonometric tables give the values, correct to four places of decimals for the angles from 0° to 90° spaced at intervals of 60′ . A trigonometric table consists of three parts.

A column on the extreme left which contains degrees from 0° to 90°, followed by ten columns headed by 0′ , 6′ , 12′ , 18′ , 24′ , 30′ , 36′ , 42′ , 48′ and 54′ .

Five columns under the head mean difference has values from 1,2,3,4 and 5.

For angles containing other measures of minutes (that is other than 0′ , 6′ , 12′ , 18′ , 24′ , 30′ , 36′ , 42′ , 48′ and 54′ ), the appropriate adjustment is obtained from the mean difference columns.

The mean difference is to be added in the case of sine and tangent while it is to be subtracted in the case of cosine.

Now let us understand the calculation of values of trigonometric angle from the following examples.

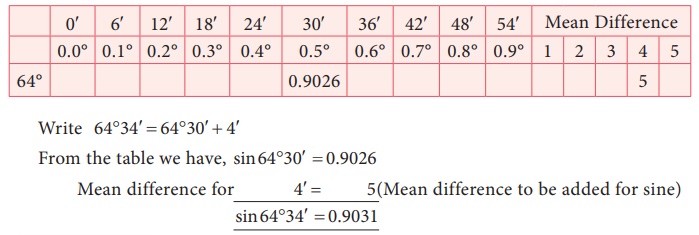
Example 6.11

Find the value of sin 64º34′.

Solution

Example 6.12

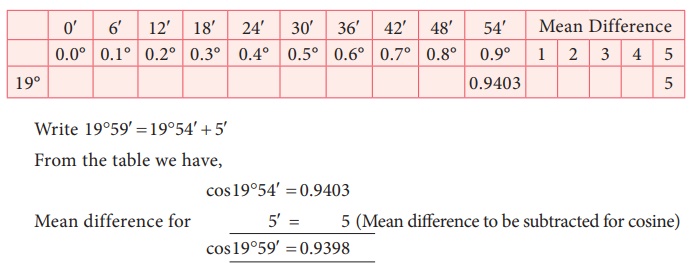
Find the value of cos19º59′

Solution

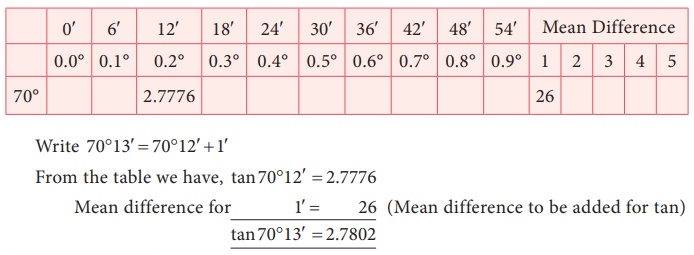
Example 6.13

Find the value of tan70º13′

Solution

Example 6.14

Find the value of (i) sin 38º36′ + tan12º12′ (ii) tan 60º25′ - cos 49º20′

Solution

(i) sin 38º36′ + tan12º12′

sin38º36′ = 0.6239

tan12º12′ = 0.2162

sin38º36′ + tan12º12′ = 0.8401

(ii) tan 60º25′ - cos 49º20′

 tan60º25′ = 1.7603 + 0.0012 = 1.7615

cos 49º20′ = 0.6521 - 0.0004 = 0.6517

tan 60º25′ - cos 49º20′ =1.1098

Example 6.15

Find the value of θ if (i) sin θ = 0.9858 (ii) cos θ = 0.7656

Solution

(i) sin θ = 0.9858 = 0.9857 + 0.0001

From the sine table 0.9857 = 80°18′

Mean difference 1 = 2′

0.9858 = 80°20′

sin θ = 0.9858 = sin80°20′

 θ = 80°20′

(ii) cos θ = 0.7656 = 0.7660 - 0.0004

From the cosine table

0.7660 = 40°0′

Mean difference 4 = 2′

0.7656 = 40°2′

cos θ = 0.7656 = cos 40°2′

 θ = 40°2′

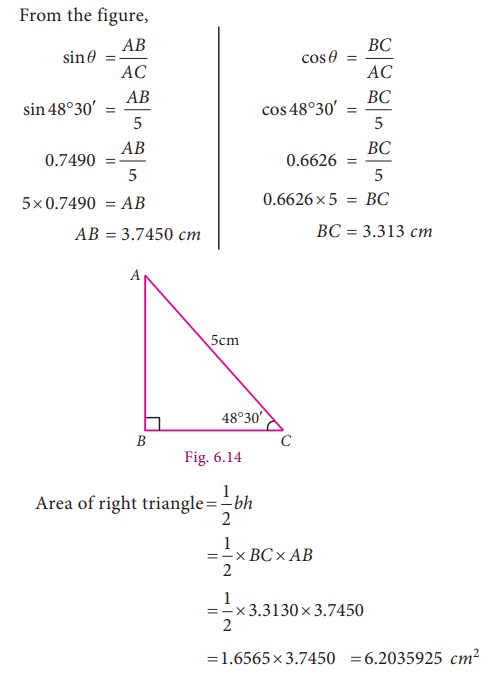
Example 6.16

Find the area of the right angled triangle with hypotenuse 5cm and  one of the acute angle is 48° 30′

Solution

Activity

Observe the steps in your home. Measure the breadth and the height of one step.

Enter it in the following picture and measure the angle (of elevation) of that step.

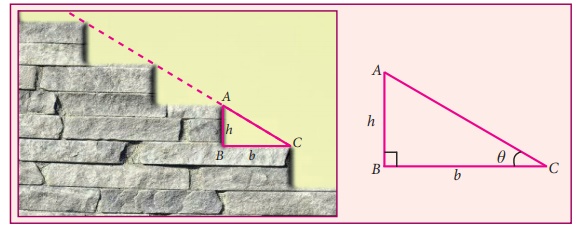
(i) Compare the angles (of elevation) of different steps of same height and same breadth and discuss your observation.

(ii) Sometimes few steps may not be of same height. Compare the angles (of elevation) of different steps of those different heights and same breadth and dicuss your observation.