Genetics Mapping by Recombination Frequencies

Mapping by Recombination Frequencies

Two or more mutations on any DNA molecule that engages in recom-bination can be approximately ordered along DNA molecules by meas-urement of the frequencies of recombination. Let us examine why this is so. Assume that the probability of a recombination or genetic cross - over between two points on two almost homologous DNA molecules is a function only of the distance between the points. Up to a limit, the greater the separation, the greater the probability of crossover. This seems reasonable because increasing the separation increases the num-ber of potential crossover sites. Recombination frequencies should be additive if the frequency is linearly proportional to marker separation. Thus, if Rf(X,Y) is the recombination frequency between markers X and

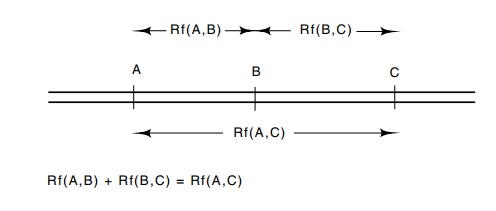
Figure 8.8 Additivity relations necessary when recombination frequency isnot linearly proportional to genetic distance.

Y, and if strict additivity holds, Rf(A,C) must equal Rf(A,B) + Rf(B,C) (Fig. 8.8).

Unfortunately, the assumption of a linear relation between recombi-nation frequency and distance is not good over extremely short or long distances. At short distances the specific nucleotides involved can gen-erate profound effects on the recombination frequencies, and additivity fails as a result. These short-distance anomalies are often called marker effects. At large distances more than one crossover is likely in the distance separating two markers. If an even number of crossovers occurs between the markers, no net recombination is observed between the markers. Therefore, as the distance between markers becomes large and multiple crossovers occur, about as many partners experience an even number of crossovers as experience an odd number. As only those with odd numbers of crossovers generate recombinants, recombination frequencies between two markers rise to 50% as an upper limit.

Given the vagaries of measuring distances by recombination frequen-cies, what can be done? Often the major question is merely one of marker order. The actual distances separating the markers are not of great importance. Three-factor genetic crosses are a partial solution. They permit ordering of two genetic markers, B and C, with respect to a third, A, that is known to lie on the outside. That is, the experiment is to determine whether the order is A-B-C or A-C-B.

Here the crosses will be described as they are performed in prokary-otes in which only one of the two participating DNA molecules is a complete chromosome, but the basic principles apply for the situation of recombination between two complete chromosomes. Mating experi-ments permit the introduction of a portion of the chromosomal DNA from a donor bacterial cell into a recipient cell in a process called bacterial conjugation. As a result of the inviability of such a linear DNA fragment, if a crossover occurs between the chromosome of the recipi-ent and the incoming chromosome fragment, a second crossover be-tween the two DNAs must also occur for the recipient chromosome not to be left open by the single crossover event (Fig. 8.9). In general, any even number of total crossovers between the incoming DNA and the recipient chromosome will yield viable recombinants.

Figure 8.9 In order that a circular chromosome not be opened by geneticrecombination, two crossovers between it and a fragment of linear DNA are necessary.

The genetic markers involved in the genetic cross, A, B, and C, can be different genes or different alleles within the same gene. In principle it does not matter, but in practice it could be difficult to ascertain the different varieties of recombinants if the markers all lie within the same gene.

To determine the gene order, compare the fraction of B⁺C⁺ recombi-nants among all the A⁺ recombinants in the two crosses (Fig. 8.10), first between an A^-B^-C⁺ chromosome and an A⁺B⁺C^- DNA fragment, and then between an A^-B⁺C^- chromosome and an A⁺B^-C⁺ fragment. If the gene order is ABC, then generation of B⁺C⁺ recombinants from the first cross requires only two crossover events, whereas the second cross requires crossovers in the same two intervals as the first plus an additional two crossovers. Therefore the fraction of the B⁺C⁺ recombinants will be much higher from the first cross. Alternatively, if the gene order is ACB, recombinants will result from the second cross.

Figure 8.10 Three-factor crosses. The first requires only two crossovers toproduce A⁺B⁺C⁺ progeny whereas the second requires four.

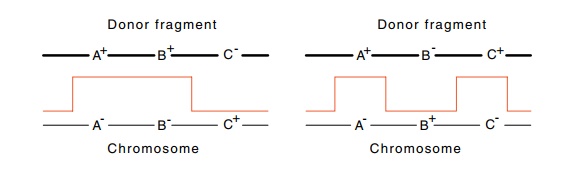
Figure 8.11 Recombination be-tween a chromosome containing a point mutation and a DNA frag-ment containing a deletion. Crossovers can occur only be-tween homologous segments, that is, outside a deleted area.a greater fraction of B⁺C⁺