Example Problems on Profit, Loss, Discount, Overhead Expenses and GST

Example Problems on

Profit, Loss, Discount, Overhead Expenses and GST

Example 4.6

Ranjith bought a washing machine for ₹16150 and paid ₹1350 for its transportation.

Then, he sold it for ₹19250. Find his gain or loss percentage.

Solution:

Total C.P of the washing machine

 = C.P + Overhead Expenses

 = 16150 + 1350 = ₹17500

S.P = ₹19250

Here, S.P > C.P. Hence, there is a gain.

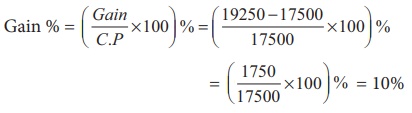
Gain % = (Gain/C.P ×100) % = { [19250 −17500]/17500 × 100 }%  = ( [1750/17500] × 100 ) % =10%

Example 4.7

If the selling price of an LED TV is equal to 5/4 of its cost price, then find the gain / profit percentage.

Solution 1:

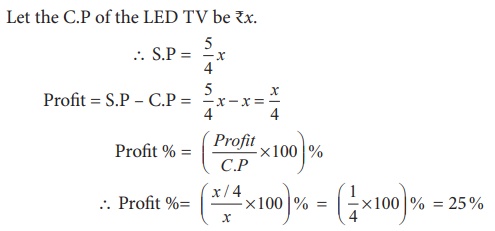
Solution 2:

Let the C.P of the LED TV be ₹x.

∴ S.P = 5/4 = x

Profit = S.P – C.P = 5/4 x − x = x/4

Profit % = (Profit/C.P ×100) %

∴ Profit % = ( x / 4 ×100) % = (1/4 ×100) % = 25%

Example 4.8

The cost price of 16 boxes of strawberries is equal to the selling price of 20 boxes of strawberries. Find the gain or loss percentage.

Solution:

Let the C.P of one strawberry box be ₹ x .

C.P of 20 strawberry boxes = 20 x and

S.P of 20 strawberry boxes = C.P of 16 strawberry boxes = 16 x (given)

Here, S.P < C.P, hence there is a loss.

Loss = C.P –S.P = 20 x - 16 x =4 x

Loss % = ( [Loss/ C . P] ×100 ) %

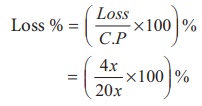
= ([4x/20x] ×100) %

∴ Loss % = 20 %

If the cost price of x articles = selling price of y articles, then profit % = 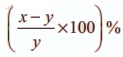= ( [x-y/y] ×100) % . If the answer is negative, then it is treated as loss. Check and verify this for Example 4.8.

Example 4.9

By selling a bicycle for ₹4275, a shopkeeper loses 5%. For how much should he sell it to have a profit of 5%?

Solution:

S.P of the bicycle = ₹4275

Loss = 5%

To have a profit of 5%, he should sell the bicycle for ₹4725.

Example 4.10

The price of a rain coat was slashed from ₹1060 to ₹901 by a shopkeeper in the rainy season to boost the sales. Find the rate of discount given by him.

Solution:

Discount = Marked Price –Selling Price

 = 1060 – 901

 = ₹159

∴ Discount % 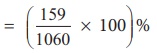= ( [159/1060] × 100) %

 = 15%

Think

A shopkeeper marks the price of a marker board 15% above the cost price and then allows a discount of 15% on the marked price. Does he gain or lose in the transaction?

Solution:

Let cost price of marker board be 100

CP = 100 Marks it 15% above CP

∴  Marked price = MP = ( [15/100] × CP ) + CP

= ( [15/100] × 100 ) + 100 = 15 + 100 = 115

Discount % = 15%

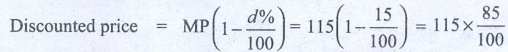
Discounted price = MP (1 – (d%/100)) = 115 (1 – (15/100)) = 115 × (85/100) = 97.75

∴ He sells it 97.75 which is less than his cost price. Therefore he loses

Loss = 97.75 − 100 = −2.25

Example 4.11

Find the single discount in percentage which is equivalent to two successive discounts of 25% and 20% given on an article.

Solution:

Let the marked price of an article be ₹100.

First discount of 25% = 100 × (25/100) = ₹25

Price after first discount = 100 - 25 = ₹75

Second discount of 20% = 75 × (20/100) = ₹15

Price after second discount = 75 - 15 = ₹60

Net selling price = ₹60

Single discount in percentage equivalent to two given successive discounts = (100–60)% = 40%.

Note

• If there are 2 successive discounts of a % and b % respectively, then

• Single discount in % equivalent to 3 successive discounts of a %, b % and c % respectively =

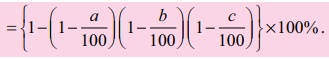
(Use this formula for the Example 4.11 and check the answer).

Example 4.12

A water heater is sold by a trader for ₹10502 including GST at 18%. Find the marked price of the water heater and GST.

Solution 1:

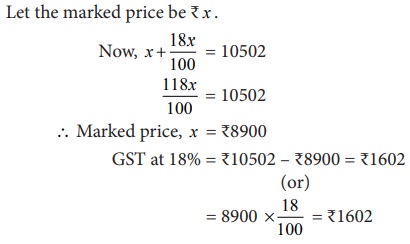
Solution 2:

Let the marked price be ₹ x .

Now, x + (18x/100) = 10502

118x / 100 = 10502

Marked price, x = ₹8900

GST at 18% = ₹10502 – ₹8900 = ₹1602

(or)

 = 8900 × (18/100) = ₹1602

Example 4.13

A family went to a hotel and spent ₹350 for food and paid extra 5% as GST. Calculate the CGST and SGST.

Solution:

Cost of food = ₹350

Extra 5% paid as GST is equally shared by the Central and the State Governments at 2.5% each.

CGST = SGST = 350 × (2.5/100) = ₹8.75