Electrostatic Forces that Determine Protein Structure - Protein Structure

Electrostatic Forces that Determine Protein Structure

Proteins have a difficult time surviving. If we heat them a little above the temperatures normally found in the cells from which they are isolated, most are denatured. Why should this be? On first consideration it would make sense for proteins to be particularly stable and to be able to withstand certain environmental insults like mild heating. One expla-nation for the instability is that proteins just cannot be made more stable. A second possibility is that the instability is an inherent part of proteins’ activities. This latter possibility seems more likely since en-zymes extracted from bacteria that thrive at temperatures near the boiling point of water frequently are inactive at temperatures below 40°. It could be that to act as catalysts in chemical reactions or to participate in other cellular activities, proteins must be flexible, and such flexibility means that proteins must exist on the verge of denaturing. A final possibility is that rapid fluctuations in structure of the folding interme-diates are necessary for a protein to find the correct folded conforma-tion. The existence of such meta-stable states may preclude the existence of a highly stable folded state. Future research should illuminate this question. For the present, we will examine the origins of the weak forces that barely manage to give proteins specific shapes.

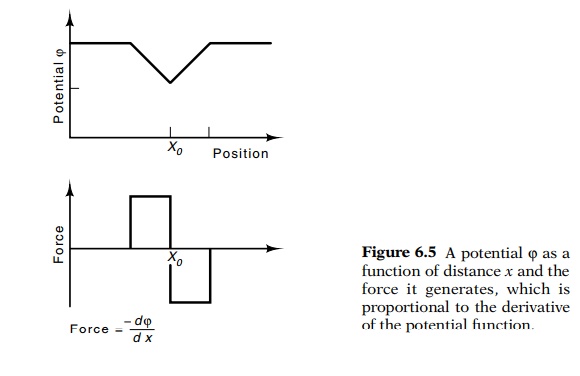
Often it is helpful to think of the interactions between amino acids in terms of forces. In some cases, physicists and physical chemists have also found it convenient to consider the interactions between objects in terms of potentials (Fig. 6.5). Some of our discussion will be more streamlined if we, also, use potentials. Forces and potentials are easily interconvertible since forces are simply related to potentials. The steep-ness of an object’s potential at a point is proportional to the force on the object while at that point,

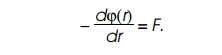
Alternatively, the potential difference between two points is propor-tional to the work required to move an object between the two points.

Figure 6.6 The electrostatic force between two charges of valueQ1andQ2separated by a distance r and the potential ϕ produced by a single charge Q1.

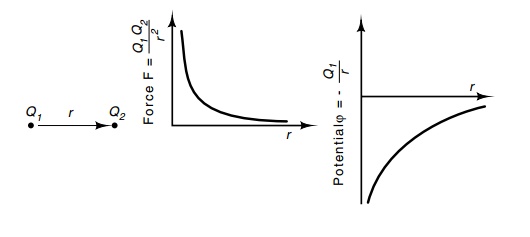
Electrostatics are the basis of several of the forces that determine protein structure. Charges of unlike sign attract each other with a force proportional to each of the charges and inversely proportional to the square of the charge separation (Fig. 6.6). The force is also inversely proportional to the dielectric constant of the medium, but for purposes of our discussion, this factor will not be considered. Thus, the potential generated at a point by a charge is proportional to the magnitude of the charge and inversely proportional to the distance of the point from the charge

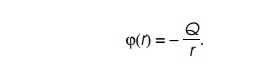
The electric field at a point is defined as the force a unit charge would feel at that point. Therefore, the magnitude of the electric field at a point r generated by a charge Q at the origin is

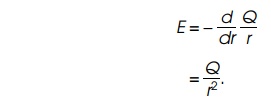
Since both positively and negatively charged amino acids exist, direct electrostatic attractions are possible in proteins. These generate what are called salt bridges. A number of proteins contain such salt bridges.

 Figure 6.7 An electrical dipole and the potential generated at a distancerfromthe dipole. Angular dependencies have been ignored.

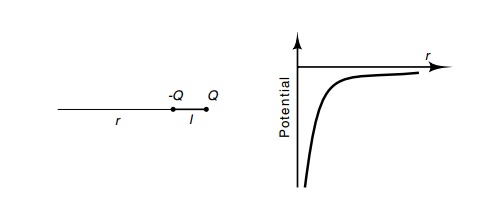
When two equal and opposite charges or partial charges are located near one another, as is found in the polar amino acids and in each peptide bond, it is convenient to view their combined effect on other atoms and molecules as a whole rather than considering each charge individually. A dipole with charges +Q and -Q separated by a distance l (Fig. 6.7) generates a potential and electric field proportional to

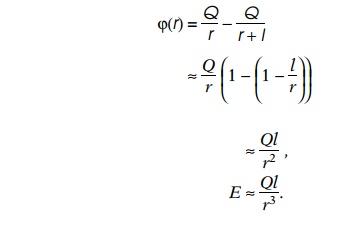
Interactions between pairs of dipoles are also common in proteins. By the same reasoning as used above, the potential between the two dipoles ql and QL can be shown to be proportional to

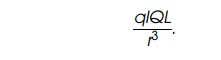
Even more important to protein structure and function than the interactions between permanent dipoles in proteins are the momentary interactions between temporary dipoles that have been created by a brief fluctuation in the positions of charges. The forces generated by interactions between such dipoles are called London dispersion forces. They are weak, short-ranged, up to an Angstrom or two, attractive forces that exist between all molecules. These form the basis of most of the selectivity in the binding of other molecules to proteins. If the shapes of a protein and another molecule are complementary, then many of these attractive forces can act and hold the two molecules tightly together. If

the shapes are not exactly complementary, then because the forces are short-ranged, only the small areas in contact are subject to dispersion attractive forces and the two molecules do not strongly bind to one another.

Dispersion forces are particularly short-ranged since their attractive potential falls off with the sixth power of the distance separating the molecules. Although these forces are best understood in the framework of quantum mechanics, we can understand the origin of the sixth-power dependence. Consider an electrically neutral nonpolar molecule. Thermal fluctuations can generate a momentary separation of its plus and

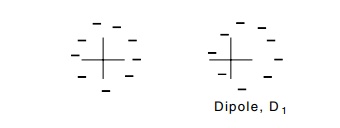
minus charges. That is, a dipole of strength D₁ = ql is briefly generated. The electric field produced by this dipole can induce a dipole in an adjacent susceptible molecule. The strength of the induced dipole is directly proportional to the strength of the local electric field. That is, the induced dipole has a strength, D₂, proportional to

Since, as discussed above, the potential between two dipoles is proportional to the product of their strength and inversely proportional to the cube of their separation,

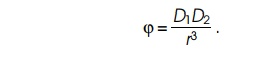
Substituting the value for D₂ in the potential yields the result that the potential between the two dipoles is inversely proportional to the sixth power of their separation,

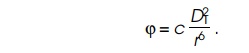
Due to the inverse sixth-power dependence, the dispersion forces become much stronger as the distance separating two molecules be-comes smaller. The force cannot become too great, for once the elec-tronic cloud of one molecule begins to interpenetrate the cloud of the other molecule, a very strong repulsive interaction sets in. It is compu - tationally convenient to approximate this repulsive potential as an inverse twelfth power of the separation of the centers of the atoms. The combination of the two potentials is known as a Van der Waals potential. The radius at which the strong repulsion begins to be significant is the Van der Waals radius (Fig. 6.8).

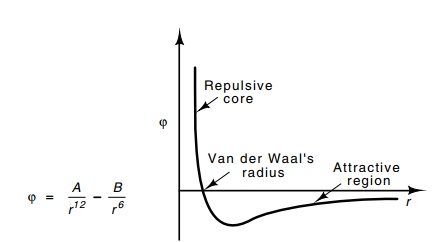
Figure 6.8 A Van der Waals potential.