Calculation of Protein Tertiary Structure

Calculation of Protein Tertiary Structure

The sequence of amino acids in a protein and the environment of the protein usually determines the structure of the protein. That is, most proteins are capable of folding to their correct conformations without the assistance of any folding enzymes. This is known from the fact that many proteins can be denatured by heat or the addition of 6 M urea and will renature if slowly returned to nondenaturing conditions. Since the sequence is sufficient to determine structure, can we predict the struc-ture? The correct folding of some proteins, however, appears to require the assistance of auxiliary proteins called chaperonins.

We can imagine several basic approaches to the prediction of protein structure. The first is simply to consider the free energy of every possible conformation of the protein. We might expect that the desired structure of the protein would be the conformation with the lowest potential energy. The approach of calculating energies of all possible conforma-tions possesses a serious flaw. Computationally, it is completely infea-sible since a typical protein of 200 amino acids has 400 bonds along the peptide backbone about which rotations are possible. If we consider each 36° of rotation about each such bond in the protein to be a new state, there are 10 states per bond, or 10⁴⁰⁰ different conformational states of the protein. With about 10⁸⁰ particles in the universe, a calculational speed of 10¹⁰ floating point operations per second (flops,

Figure 6.16 A system in state 1 is metas-table and, when equilibrium is reached, should be found in state 2. Some proteins as isolated in their active form could be in meta-stable states. Similarly, in calcu-lation of conformation, a calculation seeking an energy minimum might be-come trapped in state 1, when, in fact, state 2 is the correct conformation.

a unit of speed measure of computers), an age of the universe of roughly 10¹⁸ seconds, with one superfast computer for each particle in the universe and beginning to calculate at the origin of the universe, we would have had time to list, let alone calculate the energy of, only an infinitesimal fraction of the possible states of one protein.

The preceding example is known as the Levinthal paradox. It illus-trates two facts. First, that we cannot expect to predict the folded structure of a protein by examining each possible conformation. Sec-ond, it seems highly unlikely that proteins sample each possible confor-mational state either. More likely they follow a folding pathway in which at any moment the number of accessible conformations is highly lim-ited. We can try to fold a protein by an analogous method.This can be done by varying, individually, the structure variables like angles. As long as changing an angle or distance in one direction continues to lower the total energy of the system, movement in this direction is permitted to continue. When minima have been found for all the variables, the protein ought to be in a state of lowest energy. Unfortunately, the potential energy surface of proteins does not contain just one local minimum. Many exist. Thus, when the protein has “fallen” into a potential energy well, it is very unlikely to be in the deepest well (Fig. 6.16). This energy minimization approach has no convenient way to escape from a well and sample other conformation states so as to find the deepest well. One approach to avoiding this problem might be to try to fold the protein by starting at its N-terminus by analogy to the way natural proteins are synthesized. Unfortunately, this does not help much in avoiding local mimima or achieving the correct structures.

Yet a third way for us to calculate structure might be to mimic what a protein does. Suppose we calculate the motion of each atom in a protein simply by making use of Newton’s law of motion

F = ma.

From chemistry we know the various forces pushing and pulling on an atom in a molecule. These are the result of stretching, bending, and twisting ordinary chemical bonds, plus the dispersion forces or Van der Waals forces we discussed earlier, electrical forces, and finally hydrogen bonds to other atoms. Of course, we cannot solve the resulting equations analytically as we do in some physics courses for particularly simple idealized problems. Solving has to be done numerically. At one instant positions and velocities are assumed for each atom in the structure. From the velocities we can calculate where each atom will be 10^-14 second later. From the potentials we can calculate the average forces acting on each atom during this interval. These alter the velocities according to Newton’s law, and at the new positions of each atom, we adjust the velocities accordingly and proceed through another round of calculations. This is done repeatedly so that the structure of the protein develops in segments of 10^-14 second. The presence of local minima in the potential energy function is not too serious for protein dynamics calculations since the energies of the vibrations are sufficient to jump out of the local minima.

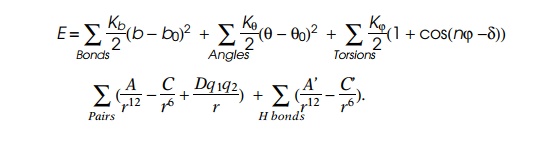
The potential function required to describe a protein, while large, can be handled by large computers. These calculations take many hours on the largest computers and can simulate the motions of a protein only for times up to 10 to 100 picoseconds. This interval is insufficient to model the folding of a protein or even to examine many of the interesting questions of protein structure.

Another useful approach with molecular dynamics is to begin with the coordinates of a protein derived from X-ray crystallography. Each of the atoms is then given a random velocity appropriate to the tempera-ture being simulated. Soon after the start of the calculations, the protein settles down and vibrates roughly as expected from general physics principles. During the course of such simulations the total energy in the system ought to remain constant, and the calculations are done with sufficient accuracy that this constraint is satisfied. The vibrations seen in these simulations can be as large as several angstroms. Frequently sizeable portions of the protein engage in cooperative vibrations.