Using a One Hot State Assignment

USING A ONE HOT STATE ASSIGNMENT

When designing with PGAS4, we should keep in mind that each logic cell contains two flip flops. This means that it may not be important to minimize the number of flip flops used in the design. Instead, we should try to reduce the number of logic cells used and try to reduce the interconnections between cells. In order to design faster logic, we should try to reduce the number of cells required to realize each equation. Using one hot state assigning will often help to accomplish this.

The one hot assignment uses one flip flop for each state, so a state machine with N states requires N flip flop. Exactly one flip flop is set to l in each state. For example a system with four (To T₁, T₂ and T₃) could use four flip flop (O₀, Q₁, Q₂ and Q₃) with the following state assignment.

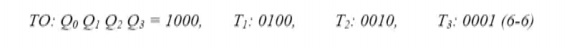
The other 12 combinations are not used.

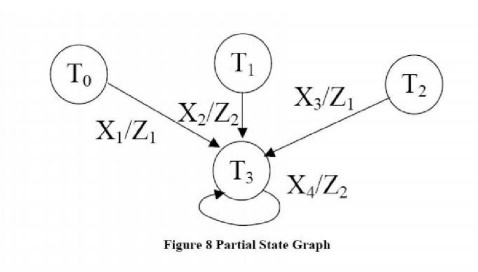
We can write next state and output equations by inspection of the graph or by tracking link parts on an SM chart consider the partial state graph . The next state equation for flip flop Q3 could be written as.

However since Q=1 implies Q1=Q2=Q3=0 the Q1=Q2=Q3 term is redundant and can be eliminated, similarly, all the primed state variables can be eliminated from the other terms, so the next state equation reduces to.

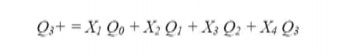
Note that each contains exactly one state variable. similarly, each term in each output equation contains exactly one state variable.

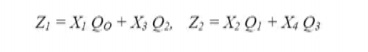
When a one hot assignment is used, the next state equation for each flip flop will contain one term for each are leading into the corresponding state (or for each link path leading into the state). In general, each term in every next state equation and in every output equation will contain exactly one state variable. The one hot state assignment for asynchronous networks is similar to that described above, but a “holding term” is required for each next state equation.

When a one hot assignment is used, resetting the system requires that one flip flop be set to 1 instead of resetting all flip flops to 0. If the flip flops used do not have a preset input (as in the case for the xilnx 3000 series), then we can modify the one hot assignment by replacing Q₀ and Q₀’ throughout. For the assignment, the modification is

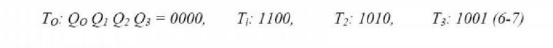
And the modified equations are:

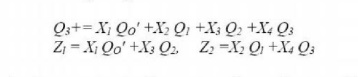
Another way to solve the reset problem without modifying the one hot assignment is to add an extra term to the equation for the flip flop, which should be 1 in the starting state. As an example, we use the one hot assignment given in (6-6) for the main dice game control. The next state equation for Q_O is

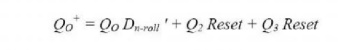
If the system is reset to state 0000 after power-up, we can add the term Q₀’Q₁’Q₂’Q₃’ to the equation for Q₀. Then, after the first clock the state will change from 0000 and 1000 (T0), Which is the correct starting state.

In general, both an assignment with a minimum number of state variables and a one hot assignment should be tried to see which one leads to a design with the smallest number of logic cells. Alternatively, if speed of operation is important, the design that leads to the fastest logic should be chosen. When a one hot assignment is used, more next state equations are required, but in general both the next state and output equation will contain fewer variables. An equation with fewer variable generally requires fewer logic cells to realize. Equations with five or fewer variables require a single cell. As seen in figure, an equation with six variables require cascading two cells, an equation with seven variables may require cascading three cells etc. The more cells cascaded, the longer the propagation delay, and the slower the operation.

STAT ASSIGNMENT RULES:  A set of heuristic rules that attempts to reduce the cost of the combinational logic in a finite state machine.

ONE HOT STATE ASSIGNMENT: State assignment uses one flip flop for each state, so a state machine with N states requires N flip flops.

1.   Reduce the following state table to the minimum number of states using successive partitioning method.

2.   Reduce the following state table to the minimum number of states using implication chart method.

3.   Use the heuristic rule on page 4 to make compact state assignment. Assign state A to “000”.

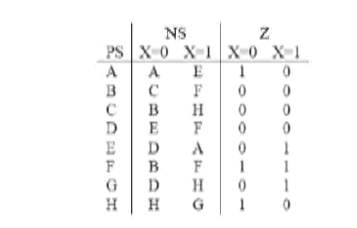
4.   Implement the following state using D flip flop and gates. Use a one hot assignment and write down the logic equations by inspecting the state table. Let S₀=001, S₁=010, and S₂=1000.

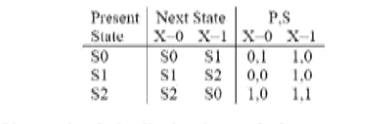
5.   Repeat problem 1 using the implication chart.

6.   Repeat problem 2 using the successive partitioning method.

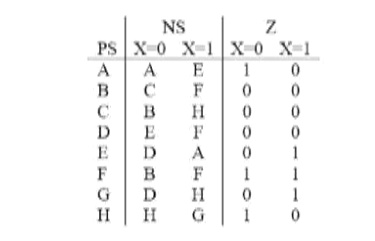
7.   Implement the state of problem 3 using one hot state assignment. Assume A=00000001, B=00000010, through H=10000000.