Equivalent States and Reduction of State Table

EQUIVALENT STATES AND REDUCTION OF STATE TABLE

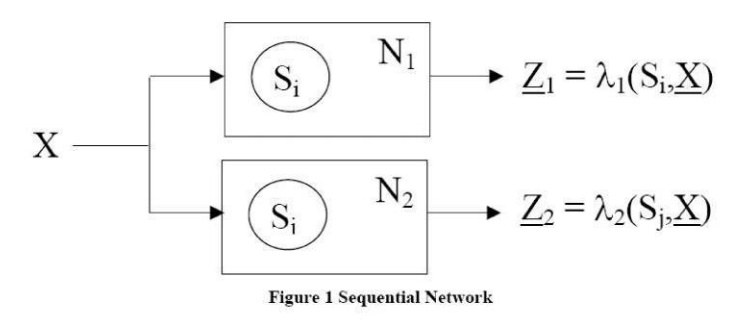
The concept of equivalent states is important for the design and testing of sequential networks. Two states in a sequential network are said to be equivalent if we cannot tell them apart by observing input and output sequences. Consider two sequential networks, N₁ and  N₂ . N₁ and N₂ could be copies of the same network. N₁ is started in state S_i and N₂ is started  in state S_j. We apply the same input sequence X to both networks and observe the output sequence Z₁ and Z₂ (the underscore notation indicates a sequence) If Z₁ and Z₂ are the same , we reset the networks to states S_i and S_j apply a different input sequence, and observe Z₁ and Z₂. If the output sequences are the same for all possible input sequences, we say that Si and S_j are equivalent (S_i=S_j). Formally, we can define  equivalent states as follows:  S_i=S_j if and only if, for every input sequence X the output sequences Z₁=ƛ₁ (S_iX) and Z₁=ƛ₂ (s_jX) are the same. This is not a very practical way to test for state equivalent since, at least in theory, it requires input sequences of infinite length, In we have a bound on number of states, then we can limit the length of the test sequences.

A more practical way to determine state equivalence uses the state equivalent theorem:

Si=Sj if and only of every single input X, the outputs are the same and the next states are equivalent. When using the definition of equivalence, we must consider all input sequences, but we do not need any information about the internal state of the system. When using the state equivalent theorem, we must look at both the output and next states, but we need to consider only single inputs rather than input sequences.

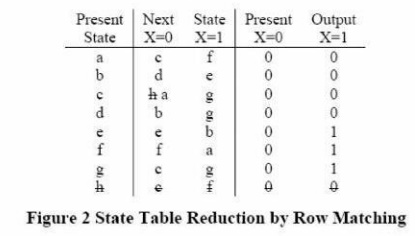
The table can be reduced by eliminating equivalent states. First, observe that states a and h have the same next states and outputs when X=0 and also when X=1. Therefore a=h so we can eliminate row h and replace h with a in the table. To determine if any of the remaining states are equivalent, we will use the state equivalent theorem. From the table, since the outputs for states a and b are the same, a and b if and only if c=d and e=f. We say that c-d and e-f are implied pairs for a-b. To keep track of the implied pairs, we make an implication chart, as shown. We place c-d and e-f in the square at the intersection of row a and column b to indicate the implication. Since states d and e have different outputs, we place an x in the d-e square to indicate that d!=e. After completing the implication chart in this way, we make another pass through the chart. The e-g so we X out the square. Similarly, since, we x out the f-g square. On the next pass through the chart, we X out all the squares that contain e-f or f-g as implied pairs (shown on the chart with dashed xs). In the next pass no additional square are X-ed  out, so the process terminates. Since all the squares corresponding to non equivalent states have been x=ed out, the coordinates of the remaining squares indicate equivalent state pairs. From the first column a= b from third column, c=d: and from the fifth column, e=f.

The implication table method of determining state equivalent can be follows:

1. Construct a chart contains a square for each pairs of states.

2. Compare each pair of rows in the state table. If the output associated with states I and j different, place an X in square i-j to indicate that i!=j. If the outputs are the same, place the implied pairs in square i-j (if the next states of I and j are m and n for some input x, then m-n is implied pair). If the outputs and next states are the same (or if i-j implies only itself), place a check (v) in square i-j to indicate that i=j

3. Go through the table square by square. If square i-j contains the implied pair m-n and square m-n contains an x, then i!=j, and an X should be placed in square i-j.

4. If any Xs were added in step3 until no more Xs are added.

5. For each square i-j that does not contain an X, i=j.

If desired, row matching can be used to partially reduce the state table before constructing the implication table. Although we have illustrated for a mealy  table, the same procedure applies to a more table.

Two sequential networks are said to be equivalent if very state in the first network has an equivalent state in the second network, and vice versa.

EQUIVALENT STATES: Two states in a sequential network are said to be equivalent if we cannot tell them apart by observing input and output sequences.

SUCCESSIVE PARTITIONING: A method for fining equivalent states by partitioning states based on outputs and next states.

IMPLICATION CHART: A tabular method for finding equivalent states based upon outputs implication made by next states.

REDUCED STATE TABLE: A state table in which all but one the equivalent states has been removed.

The next step is to make a assignment that relates the flip flops states to the states in the table. The best state assignment to use depends on a number of factors. In many cases, we should try to find an assignment that will reduce the amount of required logic. For some types of programmable logic, a straight binary state assignment will work just as well as any other. For programmable gate arrays, a one hot assignment may be perfected.

In order to reduce amount of logic required, we will make a state assignment using the following guidelines.

1.   States that have the same next state (NS) for a given input should be given adjacent assignment (look at the columns of the state table)

2.   States that are the next states of the same state should be given adjacent assignment (look at the rows)

3.   States that have the same output for a given input be given adjacent assignments.

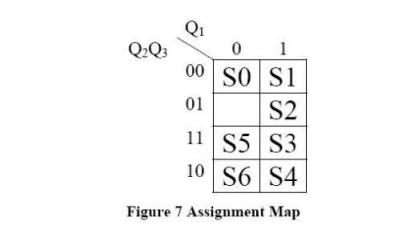
Using these guidelines tends to chump is together on the karnaugh maps for the next state and output functions . The guidelines indicates that the following states should be given adjacent assignment for the state table of Figure 6.

Figure 7 gives an assignment map, which satisfies the guidelines, and the corresponding transition table. Since state 001 is not used, the next state and outputs for this state are don’t  cares.