Subtractor using Operational Amplifier

Subtractor:

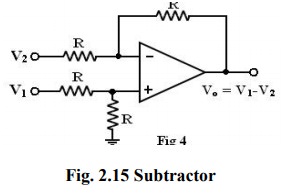
A basic differential amplifier can be used as a subtractor as shown in the above figure. If all resistors are equal in value, then the output voltage can be derived by using superposition principle.

To find the output V₀₁ due to  V₁ alone, make V₂ = 0.

Then the circuit of figure as shown in the above becomes a non-inverting amplifier having input voltage  V₁/2 at the non-inverting input terminal and the output becomes

V₀₁ =  V₁/2(1+R/R) =  V₁ when all resistances are R in the circuit.

Similarly the output V₀₂ due to V₂ alone (with  V₁ grounded) can be written simply for an inverting amplifier as

V₀₂ = -V₂

Thus the output voltage Vo due to both the inputs can be written as

V₀ =V₀₁ - V₀₂ = V₁ - V₂

Adder/Subtractor:

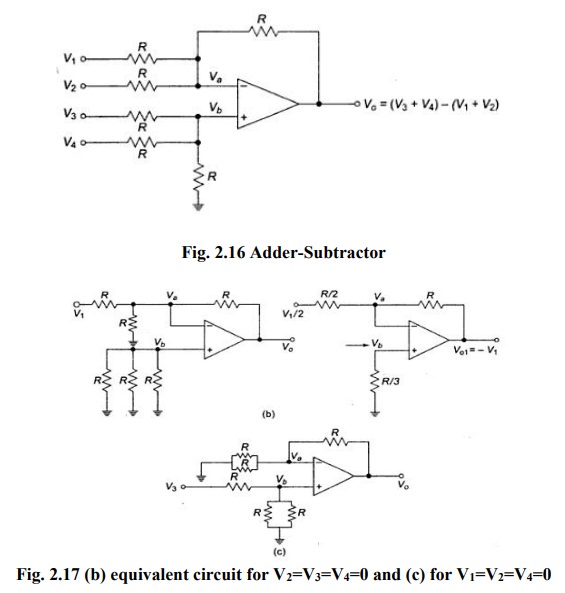
It is possible to perform addition and subtraction simultaneously with a single op-amp using the circuit shown in figure 2.16.

The output voltage Vo can be obtained by using superposition theorem. To find output voltage V₀₁ due to  V₁ alone, make all other input voltages V₂, V₃ and V₄ equal to zero.

The simplified circuit is shown in figure 2.17. This is the circuit of an inverting amplifier and its output voltage is, V₀₁= -R/(R/2) * V₁/2= -  V₁ by Thevenin‘s equivalent circuit at inverting input terminal).

Similarly, the output voltage V₀₂ due to V₂ alone is,

V₀₂= - V₂

Now, the output voltage V₀₃ due to the input voltage signal V₃ alone applied at the (+) input terminal can be found by setting  V₁, V₂ and V₄ equal to zero.

V₀₃=V₃

The circuit now becomes a non-inverting amplifier as shown in fig.(c).

So, the output voltage V₀₃ due to V₃ alone is

V₀₃ = V₃

Similarly, it can be shown that the output voltage V₀₄ due to V₄ alone is

V₀₄ = V₄

Thus, the output voltage Vo due to all four input voltages is given by

 V_o = V₀₁ = V₀₂ = V₀₃ = V₀₄

Vo = - V₁ -V₂ +V₃+ V₄

V_o = (V₃ +V₄) – (V₁ +V₂)

So, the circuit is an adder-subtractor.