Active filters using Operational Amplifier

Active filters:

An electric filter is often a frequency selective circuit that passes a specified band of frequencies and blocks or alternates signal and frequencies outside this band. Filters may be classified as

1.        Analog or digital.

2.        Active or passive

3.        Audio (AF) or Radio Frequency (RF)

1. Analog or digital filters:

Analog filters are designed to process analog signals, while digital filters process analog signals using digital technique.

2. Active or Passive:

Depending on the type of elements used in their construction, filter may be classified as passive or Active elements used in passive filters are Resistors, capacitors, inductors. Elements used in active filters are transistor, or op-amp.

Active filters offer the following advantages over passive filters:

1. Gain and Frequency adjustment flexibility:

Since the op-amp is capable of providing gain, the i/p signal is not attenuated as it is in a passive filter. [Active filter is easier to tune or adjust].

2. No loading problem:

Because of the high input resistance and low o/p resistance of the op-amp, the active filter does not cause loading of the source or load.

3. Cost:

Active filters are more economical than passive filter. This is because of the variety of cheaper op-amps and the absence of inductors.

The most commonly used filters are these:

1.        Low pass Filters

2.        High pass Filters

3.        Band pass filters

4.        Band –reject filters

5.        All pass filters.

Frequency response of the active filters:

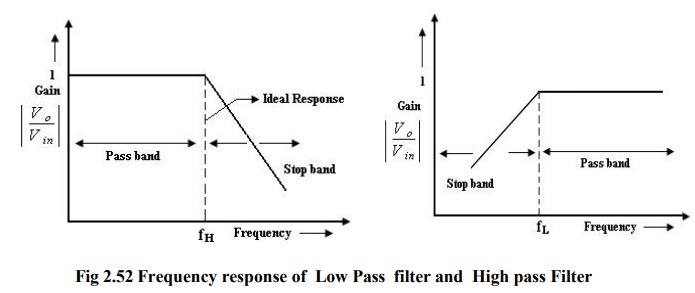
Low pass filters:

1.     It has a constant gain from 0 Hz to a high cutoff frequency f₁.

2.     At fH the gain in down by 3db.

3. The frequency between 0 Hz and fH are known as the pass band frequencies where as the range of frequencies those beyond fH, that are attenuated includes the stop band frequencies.

4.     Butterworth, Chebyshev and Cauer filter are some of the most commonly used practical filters.

5.     The key characteristics of the butter worth filter are that it has a flat pass band as well as stop band. For this reason, it is sometimes called flat- flat filters.

6.     Chebyshev filter -> has a ripple pass band & flat stop band.

7.     Causer Filter -> has a ripple pass band & ripple stop band. It gives best stop band response among the three.

High pass filter:

High pass filter with a stop band 0 <f< f _{L and} a pass band f> f _L

f_L -> low cut off frequency

f -> operating frequency.

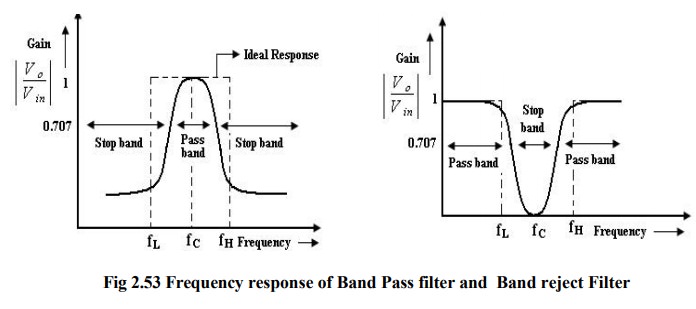
Band pass filter:

It has a pass band between 2 cut off frequencies f_H and f_L where f_H > f_L and two, stop bands: 0<f< f_L and f > f_H between the band pass filter (equal to f_H - f_L).

Band –reject filter: (Band stop or Band elimination)

It performs exactly opposite to the band pass.

It has a band stop between 2 cut-off frequency fL and fH and 2 pass bands: 0<f< fL and f> fH fC -> center frequency.

Note:

The actual response curves of the filters in the stop band either  R or  S or both with R_in frequencies.

The rate at which the gain of the filter changes in the stop band is determined by the order of the filter.

Ex:  1^st order low pass filter the gain rolls off at the rate of 20dB/decade in the stop band.

(i.e) for f > fH.

2^nd order LPF -> the gain roll off rate is 40dB/decade.

1^st order HPF -> the gain rolls off at the rate of 20dB (i.e.) until f:fL

2nd order HPF -> the gain rolls off at the rate of 40dB/decade

First order LPF Butterworth filter:

First order LPF that uses an RC for filtering op-amp is used in the non inverting configuration. Resistor R1 & Rf determine the gain of the filter. According to the voltage –divider rule, the voltage at the non-inverting terminal (across capacitor) C is,

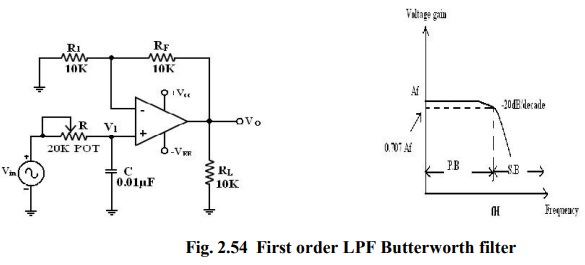
Gain A= (1+R_f/R₁)

Voltage across capacitor  V₁= V_i / (1+j2πfRC)

Output voltage V0 for non inverting amplifier =A V₁

= (1+R_f/R₁) Vi/(1+j2πfRC)

Overall gain V₀/V_i = (1+R_f/R₁) Vi/(1+j2πfRC)

Transfer function H(s) =A/(jf/f_h+1) if f_h =1/2πRC

H (jω) = A/( jωRC+1) = A/( jωRC+1).

The gain magnitude and phase angle of the equation of the LPF can be obtained by converting eqn. (1) b into its equivalent polar form as follows.

1. At very lowω)|frequency, f < fH

|H (jω) =A

2.   At f =fH

 |H (jω)| =A/√2=0.707A

3.   At f> fH

|H (jω)| <<A ≅ 0

When the frequency increases by tenfold (one decade), the volt gain is divided by 10. The gain falls by 20 dB (=20log10) each time the frequency is reduces by 10. Hence the rate at which the gain rolls off fH = 20 dB or 6dB/octave (twofold Rin frequency). The frequency f = fH is called the cut off frequency because the gain of the filter at this frequency is down by 3 dB (=20 log 0.707).

Filter design:

A LPF can be designed by implementing the following steps.

1. Choose a value of high cut off frequency f_H.

2. Select a value of C less than or equal to 1μf.

3. Choose the value of R using fh=1/2πRC

4.      Finally select values of R1 and RF dependent on the desired pass band gain AF Using A=(1+Rf/R1)

Second order LP Butterworth filter:

A second order LPF having a gain 40dB/decade in stop band. A First order LPF can be converted into a II order type simply by using an additional RC network.

The gain of the II order filter is set by R₁ and R_F, while the high cut off frequency f_H is determined by R₂, C₂, R₃ and C₃.

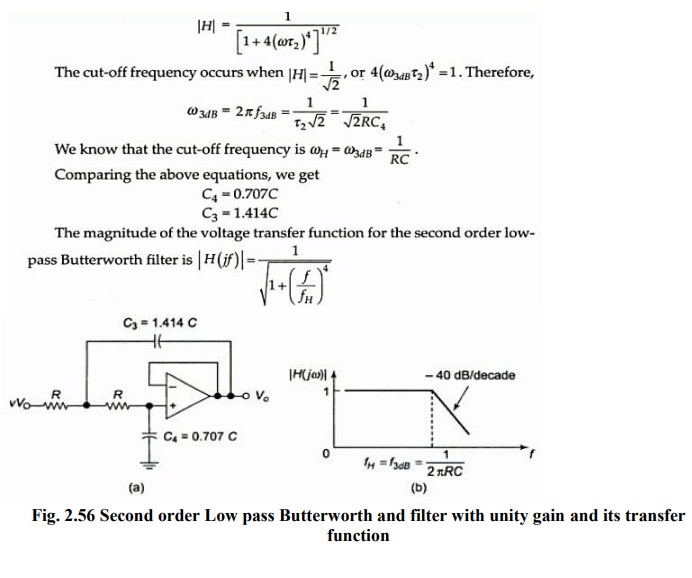
Filter Design:

1. Choose a value for a high cut off freq. (fH ).

2. To simplify the design calculations, set R₂ = R₃ = R and C₂ = C₃ = C then choose a value of C<=1μf.

3.  Calculate the value of R     R =1/2πf_hC

4. Finally, because of the equal resistor (R₂ = R₃)  and capacitor (C₂ = C₃ ) values, the pass band volt gain A_F = 1 + R_F / R₁ of the second order had to be = to 1.586. R_F = 0.586 R₁. Hence choose a value of R₁ <=100kΩ.

5.  Calculate the value of R_F.

First order HP Butterworth filter:

High pass filters are often formed simply by interchanging frequency-determining resistors and capacitors in low-pass filters.

(i.e) I order HPF is formed from a I order LPF by interchanging components R & C. Similarly II order HPF is formed from a II order LPF by interchanging R & C.

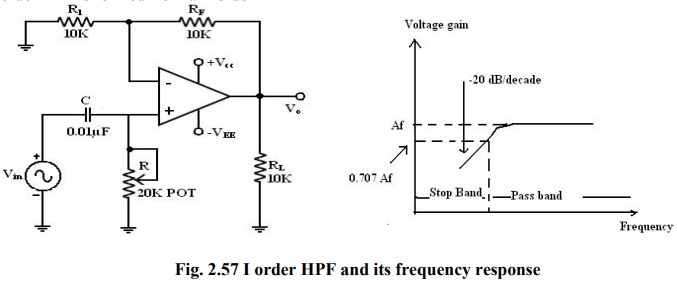
Here I order HPF with a low cut off frequency of fL. This is the frequency at which the magnitude of the gain is 0.707 times its passband value.

Here all the frequencies higher than f_L are passband frequencies.

The output voltage V₀ of the first order active high pass filter is

·           At high frequencies f>fL gain = A.

·           At f= fL gain = 0.707 A.

·           At f < fL the gain decreases at a rate of -20 db /decade. The frequency below cutoff frequency is stop band.

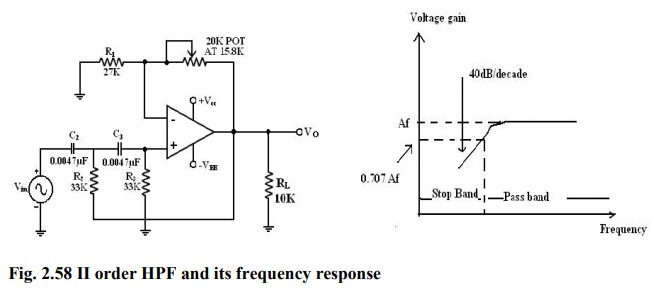
Second – order High Pass Butterworth Filter:

I order Filter, II order HPF can be formed from a II order LPF by interchanging the frequency