State Reduction & Assignment

STATE REDUCTION & ASSIGNMENT

Sometimes certain properties of sequential circuits may be used to reduce the number of gates and flip-flops during the design.

The problem of state reduction is to find ways of reducing the number of states in a sequential circuit, while keeping the external input-output relationships unchanged.

For example, suppose a sequential circuit is specified by the following seven-state diagram:

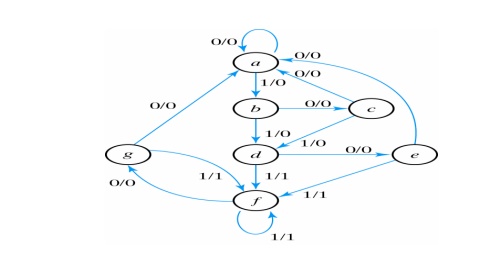
There are an infinite number of input sequences that may be applied; each results in a unique output sequence. Consider the input sequence 01010110100 starting from the initial state a:

An algorithm for the state reduction quotes that:

“Two states are said to be equivalent if, for each member of the set of inputs, they give exactly the same output and send the circuit either to the same state or to an equivalent state.”

Now apply this algorithm to the state table of the circuit:

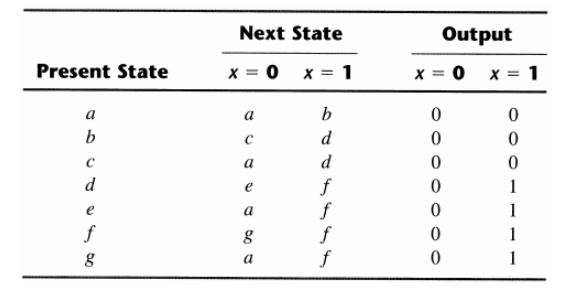
States g and e both go to states a and f and have outputs of 0 and 1 for x = 0 and x = 1, respectively.

The procedure for removing a state and replacing it by its equivalent is demonstrated in the following table:

Thus, the row with present state g is removed and stage g is replaced by state e each time it occurs in the next state columns. Present state f now has next states e and f and outputs 0 and 1 for x = 0 and x = 1. The same next states and outputs appear in the row with present state d. Therefore, states f and d are equivalent and can be removed and replaced with d.

The final reduced state table is:

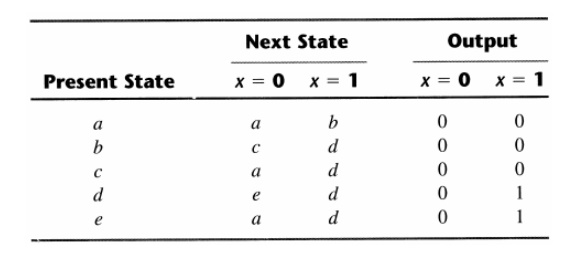
The state diagram for the above reduced table is:

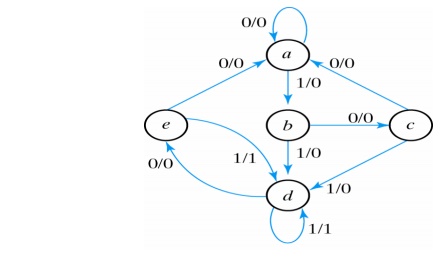
This state diagram satisfies the original input output specifications.

Applying the input sequence previously used, the following list is obtained:

Note that the same output sequence results, although the state sequence is different.